4. Докажите, что знакопостоянный ряд

, все члены которого отличны от

, сходится тогда и только тогда, когда сходится ряд

.
Из сходимости первого ряда следует стремление к нулю

, а тогда (в условиях знакопостоянства) сходится и второй просто по признаку сравнения. В обратную сторону достаточно заметить, что из стремления к нулю
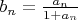
следует стремление к нулю

и, следовательно, знакопостоянство

, после чего утверждение сводится к предыдущему, т.к.

. Контрпримером может послужить, например,

(и, соответственно,

).