Бесконечный спуск Для любого целого

сумма

где

и

- натуральные числа, не равна

где

натуральное число.
Доказательство, приводимое ниже, проведено в духе утверждения самого П. Ферма о единственном способе для всех

названном им бесконечным спуском. Получено уравнение бесконечного спуска.
Положим, без ограничения общности дальнейших рассуждений, что

где

- натуральное число. Тогда сумма

, запишется в виде

![$ u^{n} + nu^{n - 1}y + [n(n - 1)/2]u^{n - 2}y^{2} + \ldots + nuy^{n - 1} + 2y^{n} = $ $ u^{n} + nu^{n - 1}y + [n(n - 1)/2]u^{n - 2}y^{2} + \ldots + nuy^{n - 1} + 2y^{n} = $](https://dxdy-03.korotkov.co.uk/f/e/6/c/e6c4d82f133bd53848c5802d6fcd0d0182.png)
![$ y^{n}(u^{n}/y^{n} + nu^{n - 1}/y^{n - 1} + [n(n - 1)/2]u^{n - 2}/y^{n - 2} + \ldots + nu/y + 2)$ $ y^{n}(u^{n}/y^{n} + nu^{n - 1}/y^{n - 1} + [n(n - 1)/2]u^{n - 2}/y^{n - 2} + \ldots + nu/y + 2)$](https://dxdy-03.korotkov.co.uk/f/2/3/5/23526b9f66a1385abb05816704cfa0f882.png)
. Обозначим

. Тогда
![$$x^{n} + y^{n}=(u + y)^{n} + y^{n}= y^{n}(w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) \ne z^{n}. $$ $$x^{n} + y^{n}=(u + y)^{n} + y^{n}= y^{n}(w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) \ne z^{n}. $$](https://dxdy-04.korotkov.co.uk/f/b/4/e/b4e08f1ee8931c695086f69ce624d26382.png)
Это утверждение доказывается от противного. Предположим, что многочлен
![$$ y^{n}F(w) = y^{n}(w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) = z^{n}$$ $$ y^{n}F(w) = y^{n}(w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) = z^{n}$$](https://dxdy-02.korotkov.co.uk/f/1/4/1/141a0ab54ec81fc0b8cf5b44b618104382.png)
![$$ F(w) = w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 = z^{n}/y^{n} = \alpha^{n}, $$ $$ F(w) = w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 = z^{n}/y^{n} = \alpha^{n}, $$](https://dxdy-04.korotkov.co.uk/f/f/1/d/f1d40d952b9e6c2360c35b75707d22a282.png)
где

рациональное положительное число.

для

Необходимо найти рациональное

, при котором

.
Согласно теоремы Декарта многочлен
![$$ F_{\alpha}(w) = w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 - \alpha^{n} $$ $$ F_{\alpha}(w) = w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 - \alpha^{n} $$](https://dxdy-03.korotkov.co.uk/f/e/b/5/eb57d673f8749d46de2bee77438f5bc082.png)
имеет только один строго положительный корень, так как

имеет всего лишь одну перемену знаков в системе своих коэффициентов [1]. Свободный член
![$$ 2 - \alpha^{n} < 0, \alpha > \sqrt[n]{2} > 1. $$ $$ 2 - \alpha^{n} < 0, \alpha > \sqrt[n]{2} > 1. $$](https://dxdy-01.korotkov.co.uk/f/0/1/3/013f309bac9d32141e713e5b101b371482.png)
Подставив, в

значение

, получим

Затем, подставив, в

значение

, получим

Так как
![$ \alpha > \sqrt[n]{2} > 1 $ $ \alpha > \sqrt[n]{2} > 1 $](https://dxdy-03.korotkov.co.uk/f/e/9/b/e9b8f816fe35aa7f696d85ae4885c3fe82.png)
, то можно записать

, где

Тогда

Значит единственный положительный корень

ногочлена

,

не является
целым числом и равен

, где

и

- рационально. Подставив

в

, получим

Представив

в виде

, где
рациональная величина

, и подставив в уравнение

, получим уравнение

Собственно говоря, уравнение
для бесконечного спуска получено. Обозначим

Можно переписать это уравнение в виде

,
т.е. замена (сдвиг)

на

или в более симметричном виде

(i1)
т.е. замена (сдвиг)

на

.
Доказательство для 
Рассмотрим уравнение (i1) при

.

(i2)
После раскрытия скобок и приведения подобных членов получаем

(i3)
Далее запишем рациональную величину

в виде

, где

- натуральные,

и

есть несократимая дробь или

есть целое большее единицы, т.е.

делится нацело на

. Ниже рассматриваются четыре
возможных вариантов значений для

и

.
1.

целое большее единицы. Умножив обе части (i3)
на 8, получим

где в правой части равенства в скобках нечетное число,
и
![$ \omega_{3} = \frac{1}{2}}\sqrt[3]{2(12\beta^{2} + 1)} $ $ \omega_{3} = \frac{1}{2}}\sqrt[3]{2(12\beta^{2} + 1)} $](https://dxdy-03.korotkov.co.uk/f/e/d/f/edf342ac27606840dd04953331e5a72282.png)
. Под корнем третьей степени стоит четное число из двух множителей, один из которых нечетное число, а другой равен 2. Кубический корень из 2 есть иррациональное число.
2.

несократимая дробь, у которой

четное, а

- нечетное.
3.

несократимая дробь, у которой
![$ q /math] и [math]$ p $ $ q /math] и [math]$ p $](https://dxdy-03.korotkov.co.uk/f/a/9/c/a9cc850c298a654ce0823f37214063f682.png)
- нечетные.
В случаях 2 и 3

![$$ \omega_{3} = \sqrt[3]{\frac{12q^{2} + p^{2}}{4p^{2}}} = \frac{1}{2p}\sqrt[3]{2p(12q^{2} + p^{2})} $$ $$ \omega_{3} = \sqrt[3]{\frac{12q^{2} + p^{2}}{4p^{2}}} = \frac{1}{2p}\sqrt[3]{2p(12q^{2} + p^{2})} $$](https://dxdy-02.korotkov.co.uk/f/9/0/1/9010acf2d32e22d29b36541beae7ad0982.png)
Под корнем третьей степени стоит четное число из трех множителей,
два из которых нечетны, так как

- нечетное, и один равен 2. Кубический корень из 2 есть число иррациональное.
Другими словами, во всех трех случаях правые части уравнений не являются кубом целого числа, так как представляют собой произведение нечетного числа на единственный четный простой множитель 2.
4.

несократимая дробь, у которой нечетное

и четное

.
Тогда, если

- нечетное или

- четное, то

Откуда

В [2] в главе 2 ЭЙЛЕР (стр. 56 - 73) рассматривается этот случай
(

и

взаимно просты и

- четно - противоположные четности или

- нечетно ).
Излагается подробное доказательство, что произведение

не равно кубу целого числа.
Таким образом доказано, что

есть число иррациональное.
Наконец сам спуск практически нетрудно построить следующим
образом. Уравнение (i1) переписывается в виде




![$ \beta[(\beta + \frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1}] + $ $ \beta[(\beta + \frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1}] + $](https://dxdy-03.korotkov.co.uk/f/a/0/b/a0b078e1d8abd2381b5ce10491232b2182.png)
![$ \frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] = \omega_{n}^{n}} $ $ \frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] = \omega_{n}^{n}} $](https://dxdy-03.korotkov.co.uk/f/6/3/2/6322ea62ecbe1ca77a7127c4e9bc26f882.png)

![$ \frac{\omega_{n}^{n}}{\beta}-\frac{1}{2\beta}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] $ $ \frac{\omega_{n}^{n}}{\beta}-\frac{1}{2\beta}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] $](https://dxdy-01.korotkov.co.uk/f/c/4/5/c45cfc76ee0da3ca778370da98c0b0f282.png)
~~~~ (j)
Рассмотрим обратный ход, т.е. подъем от

.
Уравнение (i1) для


~~~~ (j2)
Это уравнение имеет решения в рациональных числах. Например,

для целых

Совершим переход (подъем) от

к

Умножив обе части уравнения (j2) на рациональную величину

и прибавляя к этим частям рациональное выражение
![$ \frac{1}{2}[(\beta + \frac{1}{2})^{2} + (\beta - \frac{1}{2})^{2}] $ $ \frac{1}{2}[(\beta + \frac{1}{2})^{2} + (\beta - \frac{1}{2})^{2}] $](https://dxdy-04.korotkov.co.uk/f/f/3/6/f3602e959f8688745bf9dc81793fd77e82.png)
, получим

![$ \beta \omega_{2}^{2} + \frac{1}{2}[(\beta + \frac{1}{2})^{2} + (\beta - \frac{1}{2})^{2}] = $ $ \beta \omega_{2}^{2} + \frac{1}{2}[(\beta + \frac{1}{2})^{2} + (\beta - \frac{1}{2})^{2}] = $](https://dxdy-04.korotkov.co.uk/f/3/b/8/3b8a44144101c969597e8903dece332e82.png)

(j3)
Таким образом, при переходе от уравнени (j2) к уравнению (j3)(подъеме от

к

) после арифметических операций не нарушающих равенство, получается, что равенство в (j3) возможно только если

как было доказано выше, иррациональное число.
Продолжим подъем от

к

Умножив обе части уравнения (j3) на рациональную величину

и прибавляя к этим частям рациональное выражение
![$ \frac{1}{2}[(\beta + \frac{1}{2})^{3} + (\beta - \frac{1}{2})^{3}], $ $ \frac{1}{2}[(\beta + \frac{1}{2})^{3} + (\beta - \frac{1}{2})^{3}], $](https://dxdy-01.korotkov.co.uk/f/0/5/b/05b3599daf50873331b54b7aa924dfd882.png)
получим

![$ \beta \omega_{3}^{3} + \frac{1}{2}[(\beta + \frac{1}{2})^{3} + (\beta - \frac{1}{2})^{3}] = $ $ \beta \omega_{3}^{3} + \frac{1}{2}[(\beta + \frac{1}{2})^{3} + (\beta - \frac{1}{2})^{3}] = $](https://dxdy-04.korotkov.co.uk/f/f/3/1/f31b56df925fc351e39dea46a3afd4b582.png)

(j4)
Отметим, что в (j4)

есть линейная функция рационального числа

равного кубу иррационального числа

Следующая ступень подъема от

к

по аналогии с предыдущими ступенями подъема приводит к уравнению

![$ \frac{1}{2}[(\beta + \frac{1}{2})^{4} + (\beta - \frac{1}{2})^{4}] = \omega_{5}^{5} $ $ \frac{1}{2}[(\beta + \frac{1}{2})^{4} + (\beta - \frac{1}{2})^{4}] = \omega_{5}^{5} $](https://dxdy-01.korotkov.co.uk/f/8/8/9/88901415904ccd4b5327db14a12824e382.png)
~~~~~~(j5)
Если в уравнение (j5) подставить значение

из уравнения (j4), то

![$ \frac{\beta}{2}[(\beta + \frac{1}{2})^{3} + (\beta - \frac{1}{2})^{3}] + $ $ \frac{\beta}{2}[(\beta + \frac{1}{2})^{3} + (\beta - \frac{1}{2})^{3}] + $](https://dxdy-02.korotkov.co.uk/f/5/7/3/57355d3807b5cb554bde66d4c10212ba82.png)
![$ \frac{1}{2}[(\beta + \frac{1}{2})^{4} + (\beta - \frac{1}{2})^{4}] = \omega_{5}^{5}, $ $ \frac{1}{2}[(\beta + \frac{1}{2})^{4} + (\beta - \frac{1}{2})^{4}] = \omega_{5}^{5}, $](https://dxdy-02.korotkov.co.uk/f/1/1/c/11ca9809cfffad90fc72ab6c05dbf88382.png)
~~~~~~(j53)
т.е.

есть линейная функция рационального числа

равного кубу иррационального числа

Продолжая бесконечный подъем и проводя на каждом шаге преобразования, аналогичные исполненным выше, получаем,
что

есть линейная функция

Общая формула для



![$(\beta -\frac{1}{2})^{3}]+ \frac{\beta^{n-5}}{2}[(\beta + \frac{1}{2})^{4}+(\beta-\frac{1}{2})^{4}]+ $ $(\beta -\frac{1}{2})^{3}]+ \frac{\beta^{n-5}}{2}[(\beta + \frac{1}{2})^{4}+(\beta-\frac{1}{2})^{4}]+ $](https://dxdy-02.korotkov.co.uk/f/d/7/a/d7aa0b17a418f8a2eff534efd20fa10c82.png)
![$ \ldots + \frac{\beta^{2}}{2}[(\beta + \frac{1}{2})^{n - 3} + (\beta - \frac{1}{2})^{n - 3}] + $ $ \ldots + \frac{\beta^{2}}{2}[(\beta + \frac{1}{2})^{n - 3} + (\beta - \frac{1}{2})^{n - 3}] + $](https://dxdy-03.korotkov.co.uk/f/6/7/4/67479097b5c0e1e9c2ca1c0495227e6182.png)
![$ \frac{\beta}{2}[(\beta + \frac{1}{2})^{n - 2} + (\beta - \frac{1}{2})^{n - 2}] + $ $ \frac{\beta}{2}[(\beta + \frac{1}{2})^{n - 2} + (\beta - \frac{1}{2})^{n - 2}] + $](https://dxdy-02.korotkov.co.uk/f/d/4/2/d42d8c4778a5465060d3a06b23a53c3882.png)
![$ \frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] $ $ \frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] $](https://dxdy-02.korotkov.co.uk/f/9/b/f/9bfccfbb95ae28aa2414c7c17529935c82.png)
~~~~~~~~~(jn3)
или

![$ \sum_{i=4}^n \frac{\beta^{n - i}}{2}[(\beta + \frac{1}{2})^{i - 1} + (\beta - \frac{1}{2})^{i - 1}] $ $ \sum_{i=4}^n \frac{\beta^{n - i}}{2}[(\beta + \frac{1}{2})^{i - 1} + (\beta - \frac{1}{2})^{i - 1}] $](https://dxdy-04.korotkov.co.uk/f/3/3/a/33ae7a7c3b87cb41b8c110807cfe9c7782.png)
~~~~~~~~~(jn3)
История постановки и решения этой трудной задачи теории чиселИсходя из вышеизложенного, история постановки и решения этой
трудной задачи теории чисел представляется такой:
1) Сначала П. Ферма доказал утверждение для

;
2) Затем, после долгих размышлений и поисков, П. Ферма вывел из
исходного уравнения уравнение бесконечного спуска (не путать с
методом бесконечного спуска, использовавшийся самим П. Ферма для
решения других задач), которое он не записал, что породило тайну и
загадку.
Используя доказательство утверждения для

и уравнение бесконечного спуска/подъема,
справедливость утверждения для всех

и

доказал сам П. Ферма.
Общая формула для


![$ \sum_{i=5}^n \frac{\beta^{n - i}}{2}[(\beta + \frac{1}{2})^{i - 1} + (\beta - \frac{1}{2})^{i - 1}],$ $ \sum_{i=5}^n \frac{\beta^{n - i}}{2}[(\beta + \frac{1}{2})^{i - 1} + (\beta - \frac{1}{2})^{i - 1}],$](https://dxdy-03.korotkov.co.uk/f/a/5/6/a5692ffae5e56222a433f3a3ea5619a882.png)
~~~~~(jn4)
а для


![$ \frac{\omega_{4}^{4}}{\beta} - \frac{1}{2\beta}[(\beta + \frac{1}{2})^{3}+(\beta - \frac{1}{2})^{3}]$ $ \frac{\omega_{4}^{4}}{\beta} - \frac{1}{2\beta}[(\beta + \frac{1}{2})^{3}+(\beta - \frac{1}{2})^{3}]$](https://dxdy-04.korotkov.co.uk/f/b/e/7/be73c9649ebe257a3d5ad6db6c11d11b82.png)
~~~~ (j43)
Следует отметить, что само по себе уравнение бесконечного спуска/подъема, полученное из исходного,
ничего не доказывает. Только вместе с доказательством исходного утверждения для

или

это уравнение позволяет записать общую формулу

или

и

соответственно, а для любого знчения

кратного 3 или 4 общую формулу вида

и

.
I. Рассмотрим однородное диофантово уравнение вида

при этом

- целые,

Постановка задачи - принадлежат ли решения этого уравнения кольцу целых чисел

при различных значениях показателя

[2],[3],[4],[5],[6].
Нетрудно видеть, что уравнение (1) при

имеет целочисленные решения. Например, при
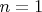
значения

и

а при
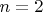
значения

и

удовлетворяют уравнению (1).
Далее утверждается, что уравнение (1) при

не имеет
натуральных решений

т.е.

.
Доказательство этой старой задачи строится от противного, что и
было изложено выше.
Расширение задачи.II. Далее, если рассматривать (1) для всех целых

, то равенство в (1) возможно только для

. Легко видеть, при

(получается 2 = 1) равенство не
выполняется.
Рассмотрим (1) с показателем степени

.

- не равные нулю целые числа.
Нетрудно видеть, что для

равенство имеет место, например, при четных равных друг другу

и

- целое.
При

и, к примеру, при

и

равенство (1) выполняется.
Пусть

, тогда (1) запишется так:

где

.
Ясно, что в (2)

.

Пусть

целое, тогда правая часть (3) есть

- ая степень целого числа. Из доказанного выше в разделе I следует, что (3) не имеет целочисленных решений для всех значений показателя степени

и, следовательно, равенство (1) не выполняется для всех

, если

- не равные нулю, целые числа.
III. Пусть в (1) для всех целых

, числа

- рациональные, т.е.

, где

- целые, не равные нулю, числа.
IV. Пусть в (1) для всех целых

, числа

- иррациональные.
V. Пусть в (1) для
всех целых

, числа

- комплексные,
т.е.

, где

, а числа

- вещественные.
Для задач III, IV, V определить условия равенства.
1. Курош А. Г. Курс высшей алгебры. М.: Наука, изд. 9-е, 1968.
2. Эдвардс Г. М. Последняя теорема Ферма. Генетическое введение в
алгебраическую теорию чисел. -М.: МИР, 1980.
3. Куликов Л. Я. Алгебра и теория чисел. -М.: Высшая школа,
1979.
4. Блинов В. Ф. Великая теорема Ферма: Исследование проблемы -М.: Изд-во
ЛКИ,2008.
5. Постников М. М. Теорема Ферма. Введение в теорию алгебраических
чисел. -М.: Наука, 1978.
6. Рибенбойм П. Последняя теорема Ферма для любителей. -М : Мир, 2003.



