Munin, по поводу уравнений движения - условия (

- оператор Любанского-Паули,

- спин,
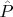
- оператор трансляций)

для
массивного поля

(A - набор спинорных индексов,

,

реализует неприводимое представление группы Лоренца, круглые скобки означают симметричность относительно перестановок индексов) эквивалентны (путем длинных преобразований это можно показать) утверждению, что поле

удовлетворяет системе уравнений

Можно показать, что для полей целого спина (рассматривая наиболее удобное из возможных представление

прочие представления данного спина можно получить из данного путем действия кое-какого оператора)

эквивалентно уравнениям

Если же взять уравнения полуцелого спина

, то из требования инвариантности относительно дискретных симметрий группы Пуанкаре можно получить систему (тут

имеет структура дираковского спинора (в частном случае n = 0 получаем его))

Для
безмассовых полей все несколько сложнее. Условия

(вектор Любанского-Паули пропорционален 4-трансляции, коэффициент пропорциональности - спиральность) эквивалентны утверждению (опять же, представления с одной спиральностью, но с разными наборами спинорных индексов связаны кое-каким оператором)

Если нужно получить теорию, инвариантную относительно дискретных симметрий, берется прямая сумма по аналогии с массивным случаем полуцелого спина (тут, однако, всегда придется ее брать, за исключением скалярного случая). Я получал из

уравнения Максвелла на тензор

и линеаризованной ОТО на тензор Вейля.
Где-то в интернете есть пособие, где это изложено подробнее, не могу пока вспомнить название.
Насчет неоднозначности - в описанный формализм оно, по-видимому, входит следующим образом: второе уравнение

не является единственно возможным, которое убирает лишние независимые компоненты поля. Другое дело, что оно может быть записано для поля любого спина, потому дело, скорее всего, в другом. Я думаю, в том, что массивные представления

связаны операторным преобразованием (аналогично - с безмассовым случаем), потому можно представить массивные частицы не одним полем, а несколькими (другое дело, что представления связаны оператором).
Про минимальность/неминимальность, думаю, можно сказать так: вид слагаемых взаимодействия, которые мы добавляем в лагранжиан, может быть подобран как в лагранжевом формализме, так и сразу в формализме уравнений движения. Вроде как, одно не имеет особых преимуществ в сравнении с другим.
Другое дело (и тут, конечно, лагранжев формализм важен), что релятивистские процессы описываются через S-оператор, который содержит лагранжиан взаимодействия, и что анализ симметрий на уровне процессов проводится через континуальное интегрирование, которое требует полный лагранжиан.