Пусть
![$g=\sqrt[5]{2}$ $g=\sqrt[5]{2}$](https://dxdy-03.korotkov.co.uk/f/a/6/3/a6377249ae5b3a7842963a15af0a431482.png)
.
Лемма 1.1
-------------
Пусть

является целым алгебраическим числом, где

- целые числа.
Тогда все числа

- чётные.
Доказательство:
---------------------
Предположим обратное, и пусть

- наименьшее целое неотрицательное число, для которого

- нечётное число.
Помножив

на

, получим, что

является целым алгебраическим числом, что невозможно, поскольку норма этого числа не является целым числом.
Лемма 1.2
--------------
Пусть

является целым алгебраическим числом, где

- целые числа.
Тогда все числа

делятся на

.
Доказательство:
----------------------
Пусть

- комплексный корень пятой степени из

.
Пусть

- сопряжённые с

числа, то есть:




Пусть

- идеал поля
![$\mathbb{Q}[g, i_5]$ $\mathbb{Q}[g, i_5]$](https://dxdy-04.korotkov.co.uk/f/b/3/f/b3fb91ff3efec6cedc172cd526bf70bb82.png)
, который является наибольшим общим делителем чисел

и

.
Числа

делятся на

, для любого целого положительного числа

, поскольку сравнимы с

по модулю

.
Следовательно,
(1)

делится на

, для любого целого положительного числа

.
Пусть

- одно из чисел

.
Пусть

.
Тогда

.
Поскольку слагаемые в выражении (1) являются сопряжёнными числами, то их сумма равна

.
Значит, из (1) следует, что

делится на

.
Поскольку

делится на

, то

делится на

.
Следовательно,

делится на

, поскольку целое рациональное число

делится на

.
Следовательно:
(2)

по модулю

.
Значит:
(3)

является целым алгебраическим числом.
Из (3) следует:
(4)

является целым алгебраическим числом.
Имеем:
(5)

,
(6)

.
Если бы правая часть равенства (6) делилась на

, то правая часть равенства (5) делилась бы на

, следовательно и левая часть равенства (5), равная

делилась бы на

, что невозможно, поскольку
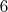
не делится на

, так как

делится на

.
Значит, правая часть равенства (6) не делится на

, следовательно левая часть равенства (6) не делится на

.
Поскольку

не делится на

, то из (4) следует, что

делится на

, и из (2) следует, что все числа

делятся на

.
Что и требовалось.
Теорема 1
---------------
Любое целое алгебраическое число

поля
![$\mathbb{Q}[g]$ $\mathbb{Q}[g]$](https://dxdy-04.korotkov.co.uk/f/7/2/a/72a24599daab8efe13972cceb995fdc982.png)
представимо в виде

, где

- целые рациональные числа.
Доказательство:
---------------------
Предположим, что это не так, и пусть
(7)

,
где

- целое алгебраическое число и

- рациональные числа, из которых не все целые.
Пусть

- дискриминант базиса

.
В силу (III),

- целые числа.
Пусть

- наименьшее целое положительное число, для которого

- целые числа.
Пусть

, где

- остаток от деления числа

на

.
Тогда

- целые числа, поскольку

для

.
Поскольку

, то
, в силу минимальности числа

.
Следовательно число

является делителем числа

.
Число

либо чётное, либо нечётное.
Рассмотрим эти два случая по-отдельности.
1. Число

- чётное.
Из (7) следует:
(8)

.
Все числа

- чётные в силу леммы 1.1.
Следовательно, числа

- целые, что противоречит минимальности числа

.
2. Число

- нечётное.
Согласно (II),

.
Поскольку

,

- нечётное число, и число

делится на

, то

делится на

.
Из (7) следует:
(9)

.
Все числа

делятся на

, в силу леммы 1.2.
Следовательно, числа

- целые, что противоречит минимальности числа

.



