дошло. Ведь любое решение уравнения из 3 переменных - это всего-лишь точка на плоскости. :D
На какой плоскости???
Любое решение уравнения от 3 переменных - это точка в 3-мерном пространстве. И уравнение задаёт много таких решений, значит, много точек. И то, что я писал выше - относится к множествам таких точек - геометрическим местам точек, удовлетворяющих уравнению, на школьном языке.
Примеры (неизвестные везде подчёркнуты):
1)

- уравнение от одной переменной, решение - одна точка

2)

- уравнение от одной переменной, решений два - две точки. (Иногда говорят, что
решение уравнения - это множество из двух точек, а каждую отдельную точку называют
корнем уравнения, это удобнее.)
3)

- уравнение от двух переменных, решений бесконечно много. Например, точка

является решением, и

является решением. Если отметить все решения на координатной плоскости, то получится линия (её можно провести по линейке между указанными точками). Это будет прямая линия - именно поэтому и говорят, что такое уравнение задаёт на плоскости прямую линию.
4)

- ещё одно уравнение от двух переменных. Решений бесконечно много, они образуют окружность. Например, решениями будут точки

- и окружность можно провести по этим точкам. Её радиус будет
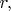
а её центр будет в точке

- осторожно, этот центр не является решением.
5)

- уравнение уже от трёх переменных, решений бесконечно много, они образуют плоскость в 3-мерном пространстве. Эту плоскость можно провести через три точки

Заметьте закономерность между примерами 1, 3, 5: каждый раз в

-мерном пространстве одно уравнение задаёт подпространство размерности

Это верно и для большего числа измерений.
В курсе аналитической геометрии изучаются, кроме того, ещё и произвольные уравнения второй степени в 2 и 3 измерениях, они дают так называемые
квадрики - кривые (на плоскости) и поверхности (в пространстве) второго порядка.
Если теперь мы возьмём систему из двух уравнений, то его решениями тоже будут точки. Поскольку в системе решение должно удовлетворять и первому уравнению, и второму уравнению, то это будут такие точки, которые входят во множество решений и первого, и второго уравнения - то есть, входят в пересечение множеств.
На плоскости: каждое из уравнений задаёт линию. Две линии пересекаются в общем случае в отдельных точках. Поэтому, система уравнений задаёт отдельные точки. Пример:

соответствует пересечению окружности (первое уравнение системы) и прямой (второе уравнение системы, прямая проходит через начало координат). Эта система задаёт две точки:

и

Это удобно записать в более общем виде

- вынос деления за скобку означает, что обе координаты делятся на одно и то же число (см. операцию умножения вектора на число).
В трёхмерном пространстве: каждое из уравнений задаёт поверхность. Две поверхности пересекаются в общем случае по линии. Поэтому, система из двух уравнений задаёт линии в пространстве. Они могут даже не укладываться в какие-то плоскости, например, линии пересечения двух цилиндров, цилиндра и конуса, цилиндра и сферы. Для частного случая двух плоскостей - линия пересечения будет прямой линией. Теперь, в систему можно добавить третье уравнение, и тогда линия пересечения двух первых поверхностей будет пересечена ещё и третьей поверхностью. И снова получатся отдельные точки.