Сферическая оболочка конечной толщины.

[schekn]

Сферическая однородная оболочка конечной толщины.

Пусть есть статическая однородная оболочка конечной толщины и вещество распределено в области $a<r<b$.
Метрику всюду ищем в "стандартной" форме, чтобы угловая функция была одинакова в трех метриках: $-r^2$. При этом у нас автоматом угловые метрические компоненты на внутренней и внешней границы сшиваются гладко. Значит, имеем такой вид метрики в трех областях ($c=1$):

$ ds^2=(1-r_g/r)dt^2-\frac{dr^2}{1-r_g/r}-r^2 d{\Omega}^2 , \quad r>b \quad (1)$

$ ds^2=e^{\nu} dt^2-e^{\Lambda} dr^2-r^2 d{\Omega}^2 \quad , a{\leqslant}r{\leqslant}b \quad (2)$

$ds^2=Adt^2-dr^2-r^2 d{\Omega}^2 \quad , r<a , \quad A=\operatorname{const} , \quad (3)$

Внешнее выражение это стандартная метрика Шварцшильда. Почему плоское пространство внутри имеет такой вид (3) будет понятно из дальнейших рассуждений. Будем сначала искать решение (2) внутри вещества. Для этого выпишем уравнения Гильберта-Эйнштейна.

$G_{0}^{0}= e^{-\Lambda}({\Lambda}' r+e^{\Lambda}-1)=8{\pi}GT_{0}^{0} \quad (4)$

$G_{1}^{1}= e^{-\Lambda}({\nu}'r+e^{\Lambda}-1)=8{\pi}GT_{1}^{1} \quad (5) $

$ G_{3}^{3}=G_{4}^{4}= e^{-\Lambda}((2{\nu}''+{\nu}'^2-{\Lambda}'{\nu}')r+2{\nu}'-2{\Lambda}')/4r = 8{\pi}GT_{3}^{3}=8{\pi}GT_{4}^{4}\quad (6)$

Уравнение (4) решается точно. Обозначая нулевую компоненту ТЭИ через плотность ${\varepsilon}$, получим решение:

$e^{\Lambda}=\frac{1}{-8{\pi}G{\varepsilon}r^2/3-C/r+1} \quad (7)$


Постоянную $C$ находим из сшивки радиальных компонент внутри оболочки с метрикой Шварцшильда на внешней границе (буду говорить - "внутри оболочки" это там где вещество, и "под оболочкой" там где плоское пространство-время):

$e^{\Lambda(b)}=1/(1-r_g/b) $ и таким образом, внутри оболочки, где вещество:

$e^{\Lambda}=\frac{r}{8{\pi}G{\varepsilon}(b^3-a^3)/3-r_g+r} \quad (8)$

В дальнейшем нам понадобится очень важное рассуждение ЛЛ-2 из пар. 100. Когда они сшивают радиальную компоненту на границе, то считают, что в данных «стандартных» координатах ${\Lambda}=0$ при $r=0$, чтобы в центре отсутствовала сингулярность, причем, не накладывается никаких специальных условий на ТЭИ, кроме сферической симметрии. Значит, радиальная компонента под оболочкой в плоском пространстве-времени автоматом получается $ g_{rr}=-1$.

Отсюда корректная сшивка на внутренней границе $r=a$ дает еще одно важное соотношение для введенной плотности вещества, а именно:

$ 8{\pi}G{\varepsilon}(b^3-a^3)/3=r_g,$ или $ \quad 8{\pi}G{\varepsilon}=\frac{3r_g}{b^3-a^3} , \quad$ $r_g=2MG \quad (9)$

То есть инвариантная плотность получилась, как отношение полной массы $M$ к объему в евклидовом пространстве.
Далее делаем еще одно допущение: поскольку оболочка статическая, то давление на внутренней и внешней границы ноль и можно предположить, что $T_{1}^{1}=0$ равно нулю для тонкой оболочки. Тогда уравнение (5):

$ e^{-\Lambda}({\nu}'r+e^{\Lambda}-1)=0 $

даёт решение для ${\nu}$ в общем виде:

${\nu}=-{\int}_{r}^{\infty}\frac{e^{\Lambda}-1}{r}dr \quad (10) $

Где

$e^{-\Lambda}=$

1. $=(1-r_g/r)^{-1}, \quad r>a \quad \quad(11a)$

2. $ =\frac{r}{8{\pi}G{\varepsilon}(b^3-a^3)/3-r_g+r},\quad a<r<b \quad (11b)$

3. $=1,\quad a<r \quad\quad(11c)$


Таким образом, согласно (10) мы получаем нулевую метрическую компоненту всюду непрерывную и даже сразу гладкую. Радиальная компонента на границах только непрерывна. В некоторых статьях теоретики допускают такое решение, когда есть разрыв первых производных на границе по координате, от которой зависят компоненты. Распишем интеграл (10):

${\nu}=-{\int}_{a}^{b}e^{\Lambda}dr/r+{\int}_{a}^{b}dr/r+{\int}_{b}^{\infty}\frac{e^{\Lambda}-1}{r}dr$

Или замечая, что последний интеграл есть: $-{\int}_{b}^{\infty}((1-r_g/r)^{-1}-1)dr/r ={\ln}{(1-r_g/b)} $ Получаем:

${\nu(r)}=-{\int}_{r}^{b}\frac{dr}{(b^3-r^3)r_g/(b^3-a^3)-r_g+r}+{\ln}(b/a)+{\ln}{(1-r_g/b)} \quad(12)$

Таким образом, найдена радиальная компонента внутри вещества. Теперь осталось найти постоянную $A=e^{\nu(a)}$ , вычисляя нулевую компоненту на внутренней границы $r=a$ .

${\nu(a)}=-{\int}_{a}^{b}\frac{dr}{(b^3-r^3)r_g/(b^3-a^3)-r_g+r}+\ln{b/a}+{\ln}{(1-r_g/b)} \quad(13)$

Теперь решение во всех трех областях с указанными допущениями найдено полностью в общем виде (1-3), (11a)-(11c), (12) , (13), оно непрерывно для всех метрических компонент, и гладко, кроме радиальной. Интеграл (12) не берется явно.

Частные случаи:

Рассмотрим тонкую оболочку $b-a=h<<b$
Найдем постоянную A в этом приближении.

${\nu(a)}=-{\int}_{a}^{b}\frac{dr}{(b^3-r^3)r_g/(b^3-a^3)-r_g+r}+{\ln}{(1-r_g/b)} \quad(14)$

Поскольку интеграл не берется явно, разложим подынтегральное выражение в ряд по малому параметру $r_g$ и проинтегрируем.

$\frac{1}{\frac{b^3-r^3}{b^3-a^3}r_g-r_g+r}{\approx}1/r+\frac{r^3-a^3}{b^3-a^3}\frac{r_g}{r^2}$

${\nu(a)}{\approx} (b-a)r_g/2a^2+{\ln}(1-r_g/a) \quad(15)

или

$A=g_{00}=e^{\nu(a)}{\approx}e^{\frac{hr_g}{2a^2}}(1-r_g/a)\quad(16)$


Найдем также массу «чистого вещества» по формуле из ЛЛ-2:

$m={\int}_{a}^{b}4{\pi}{\varepsilon}e^{\Lambda/2}r^2dr \quad(17)$

Подставляем сюда плотность ε из (9) и выражение радиальной метрической компоненты из (11b).

$m=3M{\int}_{a}^{b}\frac{r^{5/2}dr}{(b^3-a^3)\sqrt{\frac{b^3-r^3}{b^3-a^3}r_g-r_g+r}}\quad(18)$

Или приближенно $r_g<<b$ для тонкой оболочки.

$m{\approx}M(1+r_g/4b)\quad(19)$

Скалярная кривизна внутри вещества для тонкой оболочки:

$R=-\frac{3r_g}{2b^2 (b-a)}\quad(20)$


В pdf залил сюда : https://yadi.sk/i/3yYUSExFZDcdH

[epros]

И чего хотели-то?

[Munin]

Может, он считать учится. Пускай.

[schekn]

epros в сообщении #894249 писал(а):

И чего хотели-то?

Ну во-первых, может есть ошибки, я поэтому подробно все расписал,
затем эта задача давно мне не давалась, а теперь я вроде завершил решение.
Ну и по ходу дела разобрался с одним нюансом, который плохо освещен в Ландау-Лифшице.
И теперь мне по крайней мере понятно, как для оболочки определять массу самого вещества и скалярную кривизну внутри оболочки.

Munin в сообщении #894250 писал(а):

Может, он считать учится. Пускай.

Наверное Вам завидно, так как давно сами не решали подобных задач.
А вообще говоря , Вы правы, мне это было полезно.

[Munin]

schekn в сообщении #894280 писал(а):

Наверное Вам завидно, так как давно сами не решали подобных задач.

Мне не завидно. Я в подобных задачах постоянно практикуюсь. Но не считаю это чем-то настолько значительным, чтобы выкладывать на форум.

schekn в сообщении #894280 писал(а):

А вообще говоря , Вы правы, мне это было полезно.

А уж сколь полезно для вас будет дочитать учебник до конца (и проделать все упражнения, а не только одно)...

[Someone]

schekn в сообщении #894280 писал(а):

Ну во-первых, может есть ошибки, я поэтому подробно все расписал

Я тоже эту задачу решал, хотел ответить в предыдущую тему, но так и не собрался. Поэтому выкладываю написанную часть сюда. Сравнивайте и проверяйте. Обозначения несколько различаются, но переписывать такую кучу формул сложно, наверняка появится множество ошибок.

schekn в сообщении #883073 писал(а):

Я думал Вы пришли помочь, и не устраивать склоку.

Я Вам написал, почему у Вас не получилась склейка. Вы не отреагировали. Вместо того продолжилась бессмысленная дискуссия о том, в каких координатах надо склеивать. epros здесь не прав, и в этих самых "координатах кривизн" (ужасно не люблю это название) склеивать можно. Склеивать можно вообще в каких угодно координатах, их можно выбирать в каждой из склеиваемых областей независимо, лишь бы они были определены в нужном месте. Разумеется, при произвольном выборе координат склейку будет труднее описать, чем в специально подобранных.

Интервал возьмём в стандартной форме

$$ds^2=e^{\nu(r)}c^2dt^2-e^{\lambda(r)}dr^2-r^2(d\theta^2+\sin^2\theta\,d\varphi^2).\eqno(1)$$

Будем считать, что оболочка расположена в области $0<r_1<r<r_2$.
Если мы хотим, как Вы говорите, "идти от тензора энергии-импульса", то надо сначала разобраться, каким он должен быть. Рассмотрим тензор с ненулевыми компонентами следующего вида:

$$T^0_0=\rho c^2,\qquad T^1_1=-p_1,\qquad T^2_2=-p_2,\qquad T^3_3=-p_3,\eqno(2)$$

где $\rho$, $p_1$, $p_2$, $p_3$ — неотрицательные функции координаты $r$. Соответственно,

$$T_{00}=c^4e^{\nu}\rho,\qquad T_{11}=e^{\lambda}p_1,\qquad T_{22}=r^2p_2,\qquad T_{33}=r^2p_3\sin^2\theta.\eqno(3)$$

Ковариантная дивергенция этого тензора должна быть равна нулю. Вычисления дают две нетривиальные компоненты; приравнивая их к нулю, получим два уравнения

$$\begin{cases}\frac 1{2r}(2p_2+2p_3-4p_1-r\nu'(c^2\rho+p_1)-2rp_1')=0,\\ (p_3-p_2)\ctg\theta=0.\end{cases}\eqno(4)$$

Из второго уравнения сразу получаем $p_3=p_2$. Обозначая это общее значение $p(r)$, получим $p_2=p_3=p(r)$, а первое уравнение примет вид

$$4(p-p_1)-r\nu'(c^2\rho+p_1)-2rp_1'=0.\eqno(5)$$

Отметим здесь два частных случая. Если и $p_1=p(r)$ (изотропное давление), то уравнение (5) превращается в условие гидростатического равновесия, используемое при расчёте внутренней структуры звёзд:

$$p'=-\frac 12(c^2\rho+p)\nu'.\eqno(6)$$

Если же $p_1=0$, то получаем условие равновесия оболочки в виде

$$p=\frac 14c^2\rho r\nu'.\eqno(7)$$

Этот случай иллюстрируется следующим рисунком.

$$\begin{xy}/r1cm/:; (0,0)*+{\bullet};(0.6,0.8)*+{\bullet};(-0.6,0.8)*+{\bullet};(0,1)*+{\bullet}; (0,0)*\xycircle(1,1){-};(0,0)*\xycircle(0.15,0.15){-}; (-0.6,0.8);(-0.2,1.1)**@{-}*@{>}*+!RD{\bar p}; (0.6,0.8);(0.2,1.1)**@{-}*@{>}*+!LD{\bar p}; (0,1);(0,0.4)**@{-}*@{>}*+!LL{m\bar g}\end{xy}$$

Представим себе, что наша оболочка собрана из очень тонких не соприкасающихся слоёв.
Если мы выделим на слое "шапочку", то сила тяжести, действующая на "шапочку", будет уравновешиваться силами давления, приложенными к краям шапочки по касательной к слою.
Далее будем рассматривать именно этот случай.
Это не означает, что нельзя рассматривать случай $p_1(r)\not\equiv 0$. К сожалению, я не знаком с теорией упругости, и не уверен, что смогу "сходу" корректно сформулировать граничные условия на поверхностях $r=r_1$ и $r=r_2$ (вроде бы, это $p_1(r_1)=p_1(r_2)=0$, но вдруг ещё что-нибудь требуется…).

Что касается плотности материала оболочки, то её можно, например, считать постоянной. Тогда

$$\rho(r)=\begin{cases}0\text{ при }0\leqslant r<r_1,\\ \rho_0\text{ при }r_1\leqslant r\leqslant r_2,\\ 0\text{ при } r>r_2.\end{cases}\eqno(8)$$

В таком случае уравнения гравитационного поля (в смешанных компонентах) будут такими ($k$ — гравитационная постоянная):

$$\begin{cases}\frac 1{r^2}- \frac{e^{-\lambda}}{r^2}+\frac{e^{-\lambda}}r\lambda'=\frac{8\pi k\rho}{c^2},\\ \frac 1{r^2}- \frac{e^{-\lambda}}{r^2}-\frac{e^{-\lambda}}r\nu'=0,\\ \frac{e^{-\lambda}}{2r}\lambda'-\frac{e^{-\lambda}}{2r}\nu'+\frac{e^{-\lambda}}4\lambda'\nu'-\frac{e^{-\lambda}}4\nu'^2-\frac{e^{-\lambda}}2\nu''=-\frac{8\pi kp}{c^4}.\end{cases}\eqno(9)$$

Первое уравнение этой системы содержит только одну неизвестную функцию $\lambda$. Преобразуем его:

$$\frac 1{r^2}- \frac{e^{-\lambda}}{r^2}+\frac{e^{-\lambda}}r\lambda'=\frac{8\pi k\rho}{c^2}\Longrightarrow 1-e^{-\lambda}+re^{-\lambda}\lambda'=\frac{8\pi k}{c^2}r^2\rho\Longrightarrow$$

$$\Longrightarrow 1-\left(re^{-\lambda}\right)'=\frac{8\pi k}{c^2}r^2\rho\Longrightarrow\left(re^{-\lambda}\right)'=1-\frac{8\pi k}{c^2}r^2\rho\Longrightarrow$$

$$\Longrightarrow re^{-\lambda}=r-\frac{2k}{c^2}\cdot 4\pi\int\limits_0^r\tilde r^2\rho(\tilde r)d\tilde r+C_1.$$

Подставляя $r=0$ и учитывая, что $\lambda(r)$ непрерывно в точке $r=0$, получим $C_1=0$. Поэтому

$$e^{-\lambda}=1-\frac{2k}{c^2r}\cdot 4\pi\int\limits_0^r\tilde r^2\rho(\tilde r)d\tilde r.$$

Обозначая

$$\mathscr M(r)=4\pi\int\limits_0^r\tilde r^2\rho(\tilde r)d\tilde r,\eqno(10)$$

получим решение первого уравнения в виде

$$e^{-\lambda}=1-\frac{2k}{c^2r}\mathscr M(r),\qquad e^{\lambda}=\frac 1{1-\frac{2k}{c^2r}\mathscr M(r)},\eqno(11)$$

где для заданной плотности (8)

$$\mathscr M(r)=\begin{cases}0\text{ при }0\leqslant r<r_1,\\ \frac 43\pi\rho_0(r^3-r_1^3)\text{ при }r_1\leqslant r\leqslant r_2,\\ \frac 43\pi\rho_0(r_2^3-r_1^3)\text{ при }r>r_2.\end{cases}\eqno (12)$$

Предполагаем, что при $r_1\leqslant r\leqslant r_2$ выполняется неравенство $\frac{2k}{c^2}\mathscr M(r)<r$, которое в данном случае означает отсутствие горизонта событий.

Подставляя выражение (11) во второе уравнение системы (9), получим

$$\frac 1{r^2}-\frac 1{r^2}\left(1-\frac{2k}{c^2r}\mathscr M(r)\right)-\frac 1r\left(1-\frac{2k}{c^2r}\mathscr M(r)\right)\nu'=0,$$

$$\frac{2k}{c^2r}\mathscr M(r)=r\left(1-\frac{2k}{c^2r}\mathscr M(r)\right)\nu',$$

$$\nu'=\frac{2k\mathscr M(r)}{c^2r^2\left(1-\frac{2k}{c^2r}\mathscr M(r)\right)}.\eqno(13)$$

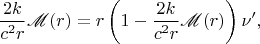
Используя условие равновесия оболочки (7), найдём давление:

$$p=\frac{k\rho(r)\mathscr M(r)}{2\left(r-\frac{2k}{c^2}\mathscr M(r)\right)}.\eqno(14)$$

В этом месте уже можно подставить все найденные величины в третье уравнение системы (9) и убедиться, что получается тождественное равенство.
Интегрируя уравнение (13), получим

$$\nu=-\int\limits_r^{+\infty}\frac{2k\mathscr M(\tilde r)d\tilde r}{\tilde r(c^2\tilde r-2k\mathscr M(\tilde r))}+C_2.$$

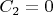
Если мы хотим, чтобы, как в решении Шварцшильда, переменная $t$ играла роль собственного времени бесконечно удалённого наблюдателя, мы должны положить $C_2=0$, и тогда

$$\nu=-\int\limits_r^{+\infty}\frac{2k\mathscr M(\tilde r)d\tilde r}{\tilde r(c^2\tilde r-2k\mathscr M(\tilde r))}.\eqno(15)$$

Подставляя (11) и (15) в выражение (1), получим искомое "склеенное" решение для оболочки. Кто-то хотел получить непрерывные коэффициенты? Ну так они здесь непрерывные, если функция $\mathscr M(r)$ непрерывна.

Рассмотрим полученное решение более подробно.

1) Область $r\geqslant r_2$.
Здесь по формуле (12) функция $\mathscr M(r)$ имеет постоянное значение

$$m=\mathscr M(r)=\mathscr M(r_2)=\frac 43\pi\rho_0(r_2^3-r_1^3),\eqno(16)$$

поэтому по формуле (11) получаем

$$e^{\lambda}=\frac 1{1-\frac{2km}{c^2r}}=\frac 1{1-\frac{r_g}r}\eqno(17)$$

(как обычно, $r_g=\frac{2km}{c^2}$ — гравитационный радиус).
Подстановка $\mathscr M(r)=m$ в формулу (15) даёт

\begin{multline*}\nu=-\int\limits_r^{+\infty}\frac{2km}{\tilde r(c^2\tilde r-2km)}d\tilde r=\int\limits_r^{+\infty}\left(\frac 1{\tilde r}-\frac{c^2}{c^2\tilde r-2km}\right)d\tilde r=\\ =\left.\ln\frac{\tilde r}{c^2\tilde r-2km}\right|_r^{+\infty}=\ln\left(1-\frac{2km}{c^2r}\right)=\ln\left(1-\frac{r_g}r\right),\end{multline*}

поэтому

$$e^{\nu}=1-\frac{r_g}r.\eqno(18)$$

Таким образом, в области $r\geqslant r_2$ интервал имеет обычный шварцшильдовский вид

$$ds^2=\left(1-\frac{r_g}r\right)c^2dt^2-\frac{dr^2}{1-\frac{r_g}r}-r^2(d\theta^2+\sin^2\theta d\varphi^2).\eqno(19)$$

2) Область $r_1\leqslant r\leqslant r_2$.
По формуле (12)

$$\mathscr M(r)=\frac 43\pi\rho_0(r^3-r_1^3),$$

поэтому по формуле (11) получаем

$$e^{\lambda}=\frac 1{1-\frac{8k\pi\rho_0}{3c^2r}(r^3-r_1^3)}.\eqno(20)$$

По формуле (15) находим (с помощью системы компьютерной математики Wolfram Mathematica)

\begin{multline*}\nu=-\int\limits_r^{r_2}\frac{2k\cdot\frac 43\pi\rho_0(\tilde r^3-r_1^3)}{\tilde r(c^2\tilde r-2k\cdot\frac 43\pi\rho_0(\tilde r^3-r_1^3))}d\tilde r-\int\limits_{r_2}^{+\infty}\frac{2km}{\tilde r(c^2\tilde r-2km)}d\tilde r=\\ =\int\limits_r^{r_2}\frac{d\tilde r}{\tilde r}+\int\limits_r^{r_2}\frac{3c^2d\tilde r}{8\pi k\rho_0\tilde r^3-3c^2\tilde r-8\pi k\rho_0r_1^3}+\ln\left(1-\frac{2km}{c^2r_2}\right)=\\ =\ln\frac{r_2}r+\sum\limits_{j=1}^3\frac{c^2}{c^2-8\pi k\rho_0\tilde r_j^2}\ln\frac{r-\tilde r_j}{r_2-\tilde r_j}+\ln\left(1-\frac{2km}{c^2r_2}\right)=\\ =\sum\limits_{j=1}^3\frac{c^2}{c^2-8\pi k\rho_0\tilde r_j^2}\ln\frac{r-\tilde r_j}{r_2-\tilde r_j}+\ln\frac{r_2-r_g}r,\qquad\qquad(21)\end{multline*}

где $\tilde r_1,\tilde r_2,\tilde r_3$ — корни уравнения

$$8\pi k\rho_0\tilde r^3-3c^2\tilde r-8\pi k\rho_0r_1^3=0\eqno(22)$$

(один из этих корней больше $r_2$, а два других либо отрицательные, либо комплексные сопряжённые с отрицательной действительной частью; в случае комплексного $\tilde r_j$ для логарифма берём значение, аргумент которого находится в интервале $(-\pi,\pi)$).

3) Область $0\leqslant r\leqslant r_1$.
В этой области

$$\mathscr M(r)=0,$$

поэтому по формулам (11) и (15) получаем

$$e^{\lambda}=1$$

и

$$\nu=\nu(r_1)=\sum\limits_{j=1}^3\frac{c^2}{c^2-8\pi k\rho_0\tilde r_j^2}\ln\frac{r_1-\tilde r_j}{r_2-\tilde r_j}+\ln\frac{r_2-r_g}{r_1},\eqno(23)$$

поэтому метрика имеет вид

$$ds^2=e^{\nu(r_1)}c^2dt^2-dr^2-r^2(d\theta^2+\sin^2\theta d\varphi^2),\eqno(24)$$

то есть, геометрия внутренней полости совпадает с геометрией некоторой области пространства-времени Минковского (чтобы получить стандартную метрику, нужно заменить временнýю координату: $t'=t\sqrt{e^{\nu(r_1)}}$).

Рассмотрим теперь случай бесконечно тонкого слоя. Для этого вычислим пределы выражений (15) и (11) при $r_2\to r_1^+$ при условии, что масса оболочки $m=\mathscr M(r_2)=\frac 43\pi\rho_0(r_2^3-r_1^3)$ остаётся постоянной. Отсюда получаем выражение для плотности $\rho_0=\frac{3m}{4\pi(r_2^3-r_1^3)}$, поэтому $8\pi k\rho_0=\frac{6km}{r_2^3-r_1^3}=\frac{3c^2r_g}{r_2^3-r_1^3}$. Заметим, что нам теперь недостаточно предположения, сделанного после формулы (12), поэтому дополнительно предположим, что выполняется неравенство $r_g<r_1$.

Начнём с вычисления предела функции $\nu$. Легко видеть из формулы (18), что при $r>r_1$

$$\lim_{r_2\to r_1^+}e^{\nu}=1-\frac{r_g}r,$$

так как при $r_1<r_2<r$ выражение $e^{\nu}$ в точности равно этому выражению. А при $0\leqslant r\leqslant r_1$ функция $\nu$ имеет постоянное значение $\nu(r_1)$, поэтому по формуле (23) её предел равен

$$\lim_{r_2\to r_1^+}\nu(r_1)=\lim_{r_2\to r_1^+}\left(\sum_{j=1}^3\frac{c^2}{c^2-8\pi k\rho_0\tilde r_j^2}\ln\frac{r_1-\tilde r_j}{r_2-\tilde r_j}+\ln\frac{r_2-r_g}{r_1}\right)=$$

(заменяем сумму соответствующим интегралом из серии равенств (21))

$$=\lim_{r_2\to r_1^+}\int\limits_{r_1}^{r_2}\frac{3c^2d\tilde r}{8\pi k\rho_0\tilde r^3-3c^2\tilde r-8\pi k\rho_0r_1^3}+\ln\frac{r_1-r_g}{r_1}=$$

(заменяем выражение $8\pi k\rho_0$ на $\frac{3c^2r_g}{r_2^3-r_1^3}$)

$$=\lim_{r_2\to r_1^+}\int\limits_{r_1}^{r_2}\frac{3c^2d\tilde r}{\frac{3c^2r_g}{r_2^3-r_1^3}(\tilde r^3-r_1^3)-3c^2\tilde r}+\ln\frac{r_1-r_g}{r_1}=\ln\left(1-\frac{r_g}{r_1}\right)-\lim_{r_2\to r_1^+}\int\limits_{r_1}^{r_2}\frac{d\tilde r}{\tilde r-r_g\frac{\tilde r^3-r_1^3}{r_2^3-r_1^3}}.$$

В последнем интеграле $0<r_g<r_1<r_2$ и $r_1\leqslant\tilde r\leqslant r_2$, поэтому $0\leqslant\frac{\tilde r^3-r_1^3}{r_2^3-r_1^3}\leqslant 1$ и $\tilde r-r_g\frac{\tilde r^3-r_1^3}{r_2^3-r_1^3}\geqslant r_1-r_g>0$, что даёт оценку для интеграла:

$$0<\int\limits_{r_1}^{r_2}\frac{d\tilde r}{\tilde r-r_g\frac{\tilde r^3-r_1^3}{r_2^3-r_1^3}}<\frac{r_2-r_1}{r_1-r_g};$$

следовательно, предел интеграла равен нулю, и мы получаем, что при $0\leqslant r\leqslant r_1$

$$\lim_{r_2\to r_1^+}\nu=\ln\left(1-\frac{r_g}{r_1}\right).$$

Таким образом, для бесконечно тонкой оболочки

$$e^{\nu}=\begin{cases}1-\frac{r_g}{r_1}\text{ при }0\leqslant r\leqslant r_1,\\ 1-\frac{r_g}r\text{ при }r>r_1.\end{cases}\eqno(25)$$

Вычисление предела для $e^{\lambda}$ не составляет труда и даёт для бесконечно тонкой оболочки

$$e^{\lambda}=\begin{cases}1\text{ при }0\leqslant r\leqslant r_1,\\ \frac 1{1-\frac{r_g}r}\text{ при }r>r_1.\end{cases}\eqno(26)$$

Таким образом,

$$ds^2=\begin{cases}\left(1-\frac{r_g}{r_1}\right)c^2dt^2-dr^2-r^2(d\theta^2+\sin^2\theta d\varphi^2)\text{ при }0\leqslant r\leqslant r_1,\\ \left(1-\frac{r_g}r\right)c^2dt^2-\frac 1{1-\frac{r_g}r}dr^2-r^2(d\theta^2+\sin^2\theta d\varphi^2)\text{ при }r>r_1.\end{cases}\eqno(27)$$

Здесь коэффициент $g_{11}=-e^{\lambda}$ имеет разрыв на поверхности склейки $r=r_1$.

schekn в сообщении #893923 писал(а):

В некоторых статьях теоретики допускают такое решение, когда есть разрыв первых производных на границе по координате, от которой зависят компоненты.

А откуда, собственно говоря, взялось требование непрерывности? Координаты "ниже" и "выше" границы склейки, вообще говоря, не связаны друг с другом, и определять непрерывность по внешнему виду формул по меньшей мере неосторожно. Например, возьмём метрику Минковского в сферических координатах

$$ds^2=c^2dt^2-dr^2-r^2(d\theta^2+\sin^2\theta d\varphi^2)$$

и в области $r>r_1$ сделаем замену радиальной координаты по формуле $r=\frac 12(r'+r_1)$, причём, "чтобы не загромождать обозначения", будем писать просто $r$ вместо $r'$. Получим

$$ds^2=\begin{cases}c^2dt^2-dr^2-r^2(d\theta^2+\sin^2\theta d\varphi^2)\text{ при }0\leqslant r\leqslant r_1,\\ c^2dt^2-\frac 14dr^2-\frac 14(r+r_1)^2(d\theta^2+\sin^2\theta d\varphi^2)\text{ при }r>r_1.\end{cases}$$

Кто-нибудь хочет сказать, что пространство-время Минковского испортилось от такой замены координат, и "склейка" стала некорректной?

Условия склейки (для случаев, когда поверхность склейки является времениподобной или пространственноподолбной), приведены в МТУ, § 21.13. Их два.
1) Обе склеиваемые области индуцируют на поверхности склейки одну и ту же метрику.
2) Если на поверхности склейки нет поверхностного слоя, то внешняя кривизна поверхности склейки в каждой из склеиваемых областей одинаковая; если же поверхностный слой есть, то скачок внешней кривизны определённым образом связан с поверхностным тензором энергии-импульса-натяжений.

[Munin]

Someone в сообщении #894305 писал(а):

Это не означает, что нельзя рассматривать случай $p_1(r)\not\equiv 0$. К сожалению, я не знаком с теорией упругости, и не уверен, что смогу "сходу" корректно сформулировать граничные условия на поверхностях $r=r_1$ и $r=r_2$ (вроде бы, это $p_1(r_1)=p_1(r_2)=0$, но вдруг ещё что-нибудь требуется…).

Мне тоже кажется так.

Someone в сообщении #894305 писал(а):

Условия склейки (для случаев, когда поверхность склейки является времениподобной или пространственноподолбной, приведены в МТУ, § 21.13. Их два.
1) Обе склеиваемые области индуцируют на поверхности склейки одну и ту же метрику.
2) Если на поверхности склейки нет поверхностного слоя, то внешняя кривизна поверхности склейки в каждой из склеиваемых областей одинаковая; если же поверхностный слой есть, то скачок внешней кривизны определённым образом связан с поверхностным тензором энергии-импульса-натяжений.

Мне больше нравится формулировка, когда рассматривается не поверхность, а область склейки, тогда нет нужды обращаться к кривизнам, и можно просто сказать, что в области склейки в обеих картах одна и та же метрика. Если устремить толщину области склейки к нулю, наверное, получится то же самое, что эти (1, 2), но это требует аккуратности и работы мозга.

[schekn]

Someone в сообщении #894305 писал(а):

Сравнивайте и проверяйте. Обозначения несколько различаются, но переписывать такую кучу формул сложно, наверняка появится множество ошибок.

Спасибо, буду проверять, но это займет некоторое время. Хорошо бы, если бы Вы оформляли данные расчеты в виде министатей в pdf, проще распечатывать.

[Munin]

schekn в сообщении #894666 писал(а):

Хорошо бы, если бы Вы оформляли данные расчеты в виде министатей в pdf, проще распечатывать.

Это вы легко можете сделать и сами, исходники-то формул все есть.

[Someone]

(Оффтоп)

schekn в сообщении #894666 писал(а):

проще распечатывать.

В левом верхнем углу, ниже заголовка темы, сразу под кнопками "новая тема" и "ответить", есть надпись "Для печати". Щёлкаете по ней. Затем в меню браузера находите пункт "Печать". Щёлкаете. Если возможности настройки печати, предоставляемые браузером, Вас не устраивают, внизу есть пункт "Печать с помощью системного диалогового окна".

[Munin]

(Оффтоп)

Вот только при этом распечатается вся тема, а не одно сообщение :-)

[Someone]

(Оффтоп)

Номера страниц надо указать. Например, текущая тема в данный момент при печати занимает 13 страниц. Моё длинное сообщение занимает страницы с 5 по 11.

[schekn]

Значит проверил, у меня получились те же формулы.
Вы более аккуратно и подробно расписали ТЭИ, тут я схалявил и действовал больше по интуиции, хотя получил то же самое, но зато я нашел массу самого вещества, что требуется для задачи epros, и скалярную кривизну на оболочке.

Что касается интеграла (21) , то у меня программа его не определила в явном виде, поэтому я оставил его как есть. Я также пытался разложить знаменатель (22) , решая кубическое уравнение, но у меня получилось одно действительное и 2 мнимых корня. Мнимость меня напугала и я решил оставить все как и было, уповая на численное взятие интеграла.

Что касается ссылки на МТУ, то конечно же спасибо, но я там ни фига не понял, зато понял, что это не учебник , а недоразумение. В учебнике должно быть все подробно расписано , приведен конкретный пример сшивки и далее можно давать задачи, как это сделано , например , у Ландау-Лифшица. Здесь же все наоборот: введены неясные постулаты, и затем задачи без всяких решений. Короче, больше не открою данный опус, только по очень сильной необходимости.
В некоторых статьях по английски эта процедура (сшивки) расписана подробно, но даже там возникают вопросы и неясности. Мне до сих пор не удается сшить коллапсирующее облако на границе в синхронных координатах. Но, это , как говорили Стругацкие, совсем другая история и для другой темы.

Что касается Энергии гравитационного поля вне оболочки, если конечно ее можно вообще определить в ОТО, то согласно ЛЛ-2 это есть "дефект масс" и вычисляется он как $M-m$. В случае , когда радиус оболочки много больше $r_g$, мои оценки дали полную "энергию" вне оболочки радиуса b:

$U=-Mr_g/4b=-M^2G/2b$

Когда радиус статической оболочки стремится к гравитационному, у меня там похожий предел, как и у Вас перед уравнением (25), я не знаю, как его находить в общем виде.

[Munin]

schekn в сообщении #895201 писал(а):

зато понял, что это не учебник , а недоразумение. В учебнике должно быть все подробно расписано

Так выглядят детские учебники, для 5 класса школы.

А серьёзные учебники, для студентов старших курсов, для аспирантов, для научных работников - ориентированы на то, что читатель умеет самостоятельно работать.

Как раз для самостоятельного и серьёзного читателя, МТУ - замечательный учебник, очень подробный и широкоохватный, по сравнению, например, с ЛЛ-2.

[SergeyGubanov]

Ещё бы для двух сфер сосчитать... Ну, поднятые камни - это уже вторая сфера.

Была хрустальная сфера, на ней лежали камни. Камни подняли и закрепили так, как Someone нарисовал:

$$\begin{xy}/r1cm/:; (0,0)*+{\bullet};(0.6,0.8)*+{\bullet};(-0.6,0.8)*+{\bullet};(0,1)*+{\bullet}; (0,0)*\xycircle(1,1){-};(0,0)*\xycircle(0.15,0.15){-}; (-0.6,0.8);(-0.2,1.1)**@{-}*@{>}*+!RD{\bar p}; (0.6,0.8);(0.2,1.1)**@{-}*@{>}*+!LD{\bar p}; (0,1);(0,0.4)**@{-}*@{>}*+!LL{m\bar g}\end{xy}$$

Теперь у нас есть две сферы: исходная хрустальная и над ней ещё одна сфера собранная из закреплённых камней. Надо вычислить минимальную работу, которую необходимо совершить для сборки второй сферы. Правда как из этого плотность энергии гравитационного поля узнать всё равно не очень понятно.