Планеты имеют не равную нулю кинетическую энергию и устойчивые дискретные орбиты с отрицательной энергией и стационарные орбиты с постоянной энергией есть.
evgeniy, оказывается, не знает, что такое положение равновесия.
Отсутствие положений равновесия в системе

взаимно притягивающихся тел доказывается очень просто.
Пусть

— равновесные положения наших тел (если какие-нибудь точки совпадают, объединим соответствующие тела в одно; тогда либо вся система сведётся к одному телу, либо останется не менее двух тел; первый случай не интересен). Равновесие означает, что сумма сил, действующих на каждое из тел со стороны остальных тел, равна

.
Для каждой пары точек

,
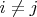
, множество точек, равноудалённых от

и

, есть плоскость, проходящая через середину отрезка

перпендикулярно ему.

точек определяют, таким образом,

плоскостей. Пусть

— точка, не принадлежащая ни одной из этих плоскостей. Тогда все

расстояний

,

, попарно различны. Пусть наибольшее расстояние получается для точки

.
Через точку

проведём плоскость, перпендикулярную отрезку

. Все остальные точки расположены с той же стороны от этой плоскости, что и точка

. Поэтому проекции всех сил, действующих на тело

, на вектор

, отрицательны, и сумма сил не может быть равна

.
Планеты имеют не равную нулю кинетическую энергию и устойчивые дискретные орбиты с отрицательной энергией и стационарные орбиты с постоянной энергией есть.
И что?
Ну давайте рассмотрим пару тел с массами

и

, вращающихся по круговым орбитам вокруг общего центра масс на расстоянии

друг от друга. Вы, надеюсь, не будете отрицать, что эти орбиты стационарные? Вычислите нам, пожалуйста, энергию этой системы. Это школьная задача. Когда вычислите, появится предмет для дальнейшего обсуждения.