Обозначим целочисленный интервал от

до

через

, множеством индексов

будем называть любое подмножество натуральных чисел

.
Набором (целых чисел)

- отображение

, принадлежащее

, тогда

- база индексов набора

,

- величина набора

, a

- сумма набора

. Набор

с базой вида

отождествим с обычным вектором

.
Поднабором

некоторого набора

, называется набор, определенный на множестве индексов

и являющийся сужением отображения

на это множество индексов

, которое включено в базу индексов

набора

, то есть:

и

(то есть

при

)
Пусть
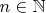
, определим для каждого натурального

функцию

дающую минимальное из таких целых неотрицательных

(если они существуют), что произвольный набор

такой величины

обладает поднабором величины

с суммой его чисел кратной

:

;

определено, если найдется хоть одно такое

, а то, что оно найдется, сейчас докажем.
Очевидно
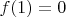
так как уже пустое множество

дает нужную сумму:

. Также очевидно

.
Для натуральных, имеющих ненулевые остатки, то есть для

имеем ограничение снизу:

(заметим, что

) так как для

есть контрпример - набор

, суммы всех поднаборов величины

которого находятся в диапазоне от 1 до

;
и также имеем ограничение сверху

, так как в этом случае среди

непересекающихся поднаборов чисел с одинаковыми остатками по

всегда найдется поднабор величины не меньше

, а сумма любых его

чисел очевидно кратна

, и продолжая выкладки получим:

,
последние неравенства следуют из

и

при

и

,
и также из

при

. Оценка сверху, как видите, не самая лучшая.
Но из этих оценок можно уже найти

:

,

,

.
Определим для любых натурального
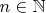
и набора

, c базой

и величиной

оператор выбора

, дающий такой поднабор

набора

величиной

и с некоторой базой

, что сумма этого поднабора кратна

, то есть:

,

и

.
Применим индукцию по делителям

и посмотрим, что можно получить.
Пусть

натуральное составное, то есть

, где

и

, тогда очевидно что

и

.
Пусть натуральное

и рассмотрим произвольный набор

- то есть, набор величины

с базой

. Докажем что

.
Выберем из набора

последовательно, по индукции, непересекающиеся поднаборов

в количестве

с базами

величиной

и суммой

каждый, то есть:

,
где

,

,

, (где

);
здесь по построению

(где

и

);
чтобы оператор

был определен для каждого

, то есть для каждого набора

величины

необходимо чтобы

,

,

- это ограничение и было взято на размер набора

.
Сформируем набор

с базой

из сумм

и поднабор

(поэлементно) с той же базой, то есть:

и

,
отсюда же

,

и значит

.
Выделяем из набора

величины

поднабор

с некоторой базой

величиной

с суммой

, что для набора

соответствует поднабору

с той же базой

и суммой

.
Но та же сумма

совпадает с суммой поднабора
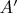
набора

имеющего базу

, действительно:

.
Значит, сумма поднабора

, а величина поднабора
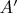
равна

.
То есть мы доказали

.
Если теперь предположить

и

, то получим

и учитывая

получим

или же

.
Теперь можно провести индукцию.
Предикат индукции

.
Начало индуции: допустим, что

выполняется для всех простых

, то есть

; для
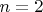
уже доказано.
Шаг индукции сделаем, либо по числу простых множителей натурального числа:

,
либо по его собственной величине:

.
Тогда доказываем общее утверждение:

, или

.
Но у нас осталось недоказанным данное утверждение для всех простых чисел.
Я отрицаю возможность того, что простота числа

как-то поможет доказать
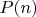
. Индукцией

данное утверждение доказать нельзя - из-за наличия модуля от

, индукция могла пройти (и прошла) только по делителям.
И моя интуиция меня не подвела. Когда я уже получил в общих чертах изложенное выше, неполное решение (оно довольно просто, просто много формализма), я увидел просто элементарное доказательство без всяких недоказанных предположений. Индукцию нужно вести не по

, а по остаткам!!! Рассмотреть для каждого

отдельно наборы из

чисел с остатками от

до

, где

и провести индукцию по

!...
Дальше сами допрете, устал я уже расписывать.



