Сложная задача по классической механике

[Kirill_Sal]

Доброго времени суток.

Есть задача: рассмотреть колебания линейной цепочки частиц, связанных упругими силами, масса которых возрастает по закону арифметической прогрессии. Надо найти спектр колебаний (или дисперсионное уравнение).

Записываем д/у с граничными условиями:

$nm(X_n)'' + k(2X_n - X_{n-1} - X_{n+1}) = 0$
$X_{N+1}=0$
$X_0=0$

Ищем решение в виде:

$X_n=(A_n)e^{iwt}$

Для определения $A_n$ получаем рекуррентное уравнение:

$(2k-nmw^2)A_n = k(A_{n-1} + A_{n+1})$

Можно рассматривать функцию $A_n=A_n(f)$ от фазы волны. Например, в случае одинаковых частиц $A_n=Ae^{-\inf}$. Нам надо решить рекуррентное уравнение так, чтобы n сократилось и осталось бы дисперсионное уравнение для $w(f)$. Похожие уравнения с суммой "ближайших соседей" есть в теории функций Бесселя. Логично предположить, что $A_n$ должны иметь иметь какую-то связь с функциями Бесселя. Однако угадать ее вид весьма непросто, тем более сложно понять, действительно ли при определенной подстановке из уравнения "уйдет" n. Из физических соображений понятно только, что $A_n$ должна стремиться к нулю при неограниченном увеличении n. Еще нельзя забывать о граничных условиях. Как дорешать задачу?

[Munin]

Можно представить себе, что это полярная система координат. Там да, Бессель.

[Kirill_Sal]

Что вы имеете ввиду?
Реккурентное соотношение для функций Бесселя имеет вид:
$(2n/x)J_n = J_{n-1} + J_{n+1}$.

[Kirill_Sal]

Я нашел вид $A_n(w^2)$. Дальше, подставляя полученное решение в рекуррентное соотношение, мы действительно получаем уравнение для $w$? Это не будет тождеством?

[Kirill_Sal]

Кажется, разобрался. Находим вид $A_n(w^2)$ из рекуррентного соотношения:

$A_n(w^2)=c_1J_{n-2(w/w_0)^2}(-2(w/w_0)^2) + c_2Y_{n-2(w/w_0)^2}(-2(w/w_0)^2)$

Приравниваем эту функцию нулю на границах цепочки. Из условия $A_0(w^2)=0$ находим связь между константами. Из условия $A_{N+1}(w^2)=0$ находим спектр колебаний. Вроде противоречий нет. Как для проверки узнать кол-во корней последнего уравнения?

Интересно, есть ли возможность введения какой-то дисперсионной зависимости?

[svv]

Kirill_Sal
Вы сделали много правильных и полезных вещей. Перенумеровали частицы так, что неподвижные крайние имеют номера $0$ и $N+1$ (я сделал бы точно так же). Заменили координату на смещение относительно положения равновесия. Ввели обозначение $\omega_0^2=\frac k m$. А вот идея использовать здесь цилиндрические функции мне кажется малопродуктивной. Функции Бесселя и Неймана с хитрым нецелым и неполуцелым порядком. Что можно с ними сделать? Разложить в ряд, записать интегральное представление? Самое лучшее — это определить их рекуррентной формулой, что возвращает нас к исходной точке.

Обозначим ещё $\lambda=\frac{\omega^2}{\omega_0^2}$. Амплитуды буду обозначать $x_k$, количество подвижных частиц $n$. Тогда уравнения примут вид:
$-x_{k-1}+(2-k\lambda)x_k-x_{k+1}=0\;,\quad k=1..n$

Запишем систему в матричной форме. Чем писать для произвольного $n$ c многоточиями, будет нагляднее, если я возьму небольшое конкретное $n$, например $n=5$.
$\begin{bmatrix} 2-1\lambda &-1&0&0&0\\-1& 2-2\lambda &-1&0&0\\0&-1& 2-3\lambda &-1&0\\0&0&-1& 2-4\lambda &-1\\0&0&0&-1& 2-5\lambda \end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{bmatrix}=\begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}$
Обратите внимание, что в такой записи из системы исчезли какие-либо параметры (вроде массы или жесткости), кроме разве что количества частиц $n$.
У нас получилась обобщённая задача о собственных значениях/векторах $A\mathbf x=\lambda B\mathbf x$.

Это однородная система. Она имеет нетривиальное решение, только если определитель матрицы равен нулю. Это и дает уравнение для определения спектра:
$\begin{vmatrix} 2-1\lambda &-1&0&0&0\\-1& 2-2\lambda &-1&0&0\\0&-1& 2-3\lambda &-1&0\\0&0&-1& 2-4\lambda &-1\\0&0&0&-1& 2-5\lambda \end{vmatrix}=0$

Обозначим такой определитель $n$-го порядка через $D_n$. Так как $D_n$ имеет специальный вид, можно продвинуться в его вычислении. Разложив $D_n$ по последней строке, получим (Вы это легко сами проделаете) рекуррентную формулу
$D_n=(2-n\lambda)D_{n-1}-D_{n-2}$
При этом $D_1=2-\lambda$ и по определению $D_0=1$.
Итак, определители для различных $n$ связаны рекуррентной последовательностью.

$D_n$ представляет собой полином $n$-й степени от $\lambda$, поэтому уравнение $D_n(\lambda)=0$ имеет $n$ корней $(\lambda_i)_{i=1}^n$ с учетом кратности. Каждый $\lambda_i$ подставляйте в систему и находите соответствующий ему собственный вектор $\mathbf x_i$.

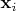
Хочу подчеркнуть, что собственные векторы, соответствующие различным собственным значениям, будут совсем непохожи друг на друга. Мне показалось, что Вы забыли о том, что здесь будет $n$ различных по характеру колебательных мод.

[ewert]

svv в сообщении #879690 писал(а):

Это однородная система. Она имеет нетривиальное решение, только если определитель матрицы равен нулю. Это и дает уравнение для определения спектра:
$\begin{vmatrix} 2-1\lambda &-1&0&0&0\\-1& 2-2\lambda &-1&0&0\\0&-1& 2-3\lambda &-1&0\\0&0&-1& 2-4\lambda &-1\\0&0&0&-1& 2-5\lambda \end{vmatrix}=0$

Это -- дискретный аналог уравнения Эйри $-y''=\lambda xy$. Соответственно, для нижней части спектра легко выписывается асимптотика при $n\to\infty$ как собственных векторов, так и собственных чисел. Правда, и выражаться она будет лишь через функции Эйри и их корни.

[Munin]

svv в сообщении #879690 писал(а):

А вот идея использовать здесь цилиндрические функции мне кажется малопродуктивной. Функции Бесселя и Неймана с хитрым нецелым и неполуцелым порядком. Что можно с ними сделать? Разложить в ряд, записать интегральное представление? Самое лучшее — это определить их рекуррентной формулой, что возвращает нас к исходной точке.

Или наплевать на рекурретные формулы, и посмотреть формулы для их нулей в общем виде. Нам же дисперсия нужна?

ewert в сообщении #879701 писал(а):

Правда, и выражаться она будет лишь через функции Эйри и их корни.

Почему-то мне поначалу показалось - Эйри, но потом я пригляделся, и подумал - Бессель. Вообще, мне, похоже, вредно думать. Посижу в сторонке.

[svv]

Ну, есть формулы для нулей цилиндрических функций. Понятна их полезность в случае цилиндрического резонатора, где дело сводится к нахождению корней $J_n(z)=0$ или $J'_n(z)=0$. Неймана нет в силу регулярности на оси. Но тут же должна быть равна нулю линейная комбинация Бесселя и Неймана, в которой мало того что и аргумент и порядок зависят от $\omega$, так ещё и коэффициенты неизвестны.

[Munin]

Давайте посмотрим сначала, что будет для Бесселя и без стенок резонатора.

[svv]

Формулы есть, например, во втором томе Бэйтмена и Эрдейи, в параграфе 7.9 «Нули функций Бесселя», но там ещё надо вчитываться.

[Munin]

Ну вот я понадеялся на то, что вы уже :-)

[ewert]

svv в сообщении #879749 писал(а):

Формулы есть, например, во втором томе Бэйтмена и Эрдейи, в параграфе 7.9 «Нули функций Бесселя»

Ну какие там могут быть формулы? Разве что асимптотики.

[Kirill_Sal]

Идея с использованием функций Бесселя позволяет нам получить относительно простое уравнение для спектра колебаний. В этом уравнении помимо $w^2$ фигурируют только характеристики $k$, $m$ и кол-во частиц $N$. Коэффициентов там нету, т.к.из первого граничного условия мы нашли связь между $c_1$ и $c _2$.

Рекуррентное соотношение для определителей, выведенное вами, тоже имеет Бесселевскую природу. Выразить многочлен $D_n$ через $D_1$ и $D_0$ - это довольно непростая задача. Нам опять-таки приходится решать рекуррентное уравнение. И по всей видимости получается тоже самое, что получил я из граничных условий. С такой же зависимостью порядка и аргумента от $w^2$.

Про различные моды я вроде не забывал. Я не ищу собственные векторы. Я ищу уравнение для $w$.

[svv]

Я его записал.

Вы же всё равно это численно будете решать? Здесь, в отличие от амплитуд, есть приятный момент. При выбранном пробном значении $\lambda$ рекуррентные формулы немедленно приводят к $D_n$, потому что начальные значения, $D_0$ и $D_1$, известны.

-- Ср июн 25, 2014 16:55:35 --

Для полиномов Чебышёва имеется явная формула $T_n(x)=\sum\limits_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k} (x^2-1)^k x^{n-2k}$, но во многих ситуациях я предпочту ей рекуррентную $T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x)$.