g______dДа, хороший пример. Я вспомнил, благодаря вам, ещё один. Где-то у Прасолова было написано в «Наглядной топологии для школьников», что если

— трилистник, а

незаузленная окружность, то

и

не гомеоморфны; впрочем, доказательства он не приводил. Если есть более-менее несложное доказательство этого факта, было бы хорошо.
Мне вот ещё что непонятно, в Зориче т.1 в «теореме о ранге» (с.493-494) в самом начале пишут: «Чтобы не менять нумерацию будем считать, что в любой точке

главный минор порядка

, стоящий в левом верхнем углу якобиевой матрицы отображения

отличен от нуля.» Так считают, в силу предположения о том, что

(

окрестность в

). И мне не очень понятно, почему это вдруг должна существовать «единая» перенумерация для всех точек из

при которой ранг матрицы

реализовывался бы в первых

строках? Может в какой-то точке нужно для этого оставить всё как есть, а в какой-то поменять первую и третюю строчку. Сформулирую построже:
4) Пусть

—

-гладкое (
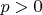
) отображение из области

(окрестности точки

) ранга

(в любой точке

), всегда ли существует такая перестановка координат

и

и окрестность

, что главный минор порядка

, стоящий в левом верхнем углу матрицы

отличен от нуля в любой точке окрестности

?