Вы ведь, ссылаясь на Пуанкаре, утверждаете, что "теория Лоренца — Пуанкаре" якобы требует наличия абсолютной системы отсчёта, а Пуанкаре это отрицает.
Вы Пуанкаре с Эйнштейном, часом, не перепутали? Это Эйнштейн заявил, что никакой АСО не существует, и тем самым полностью закрыл вопрос. После чего ему было бы крайне странно задаваться вопросом о возможности обнаружения абсолютного движения.
Пуанкаре же говорит только о невозможности обнаружения абсолютного движения (Вами приведенная цитата):
Я разыскал работу А. Пуанкаре "О динамике электрона". Вот цитата (конец § 7):
Итак, гипотеза Лоренца будет единственной, которая согласуется с невозможностью доказательства абсолютного движения…
тем самым подразумевая наличие АСО. Согласитесь, представление об отсутствии АСО и представление о невозможности обнаружения АСО в силу определенных причин – два совершенно различных представления.
ситуацию нужно рассматривать в мгновенно сопутствующей системе отсчёта, где нужная коллинеарность соблюдается.
Совершенно верно, о чем, собственно, и толкую. В сопутствующей ИСО' при нулевой скорости тела коллинеарность соблюдается независимо от направления приложения силы. И при переходе в другую ИСО (имеется в виду наблюдение из другой ИСО за приложением силы

и ускорением тела

в сопутствующей ИСО') коллинеарность этих векторов сохраняется.
А вот если воздействовать силой

на движущееся тело (покоящееся относительно ИСО') из другой ИСО, то в общем случае коллинеарность векторов не соблюдается и ускорение тела

произойдет под некоторым углом к вектору воздействия. Причем, величина этого угла не зависит от величины прикладываемой силы.
То, что Вам кажется "очевидным", в СТО просто неверно.
...
А в других ИСО из-за изменения одновременности всё становится "перекошенным", интуиция запутывается, поскольку опыта обращения с релятивистскими объектами у нас нет, и подсказывает неверные выводы.
Оставьте это для первокурсников. Лучше один раз увидеть, чем сто раз услышать. Просто с помощью формул:


строим на графике эллипсоид разлета частиц (при

) из начала координат ИСО' с той же скоростью

:
И без расчетов видно, что ось

представляет собой касательную к эллипсоиду. Таким образом можно сделать вывод о том, что при приложении силы в направлении оси

из ИСО' или в направлении оси

в сопутствующей ИСО'', ускорение пробного тела в любом случае должно происходить в направлении оси

, иначе нарушатся законы сохранения энергии и импульса.
Т.е. при ускорении тела в направлении положительных значений оси

, наблюдаемая из ИСО скорость тела
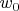
должна уменьшаться, а в направлении отрицательных значений – должна увеличиваться. Приходится констатировать, что при ускорениях принцип относительности не нарушается, а АСО остается необнаружимой.
Похоже, что с помощью известных средств абсолютное движение необнаружимо. Остается только надеяться на неизвестные пока средства, что-нибудь вроде передачи мгновенного сигнала.