Единственен ли единичный элемент в линейном пр-ве?

[tetroel]

Собственно, вопрос такой — является ли существенным для определения линейного пространства тот факт, что существует единственный единичный элемент, для которого $1\cdot \overline{x} = \overline{x}\cdot 1 = \overline{x}$? Да/нет, и, самое главное, почему?
Вопрос интересен в том контексте, можно ли, если это так, на основании существования нескольких единичных элементов доказать, что пространство не является линейным?

[provincialka]

В линейном пространстве не задано умножение элементов друг на друга. Так что единичный элемент - элемент того поля, над которым это пространство рассматривается. В поле он, конечно, один.

А чем у вас отличается умножение слева и справа?

[tetroel]

Ну, это дополнительный намёк на ассоциативность умножения на скаляр, конечно же, ничем умножение слева не отличается от умножения справа.
Но я вас понял, я уже кое в в каких формулировках не прав изначально.

Хорошо, а как тогда решить задачу о том, образует ли линейное пространство множество векторов $\mathfrak{X}=\left(x_1, x_2...x_n\right)$, у которых все координаты $x_i$—целые, если сложение задано как $x+y=\left(x_1 + y_1, x_2+y_2, ..., x_n+y_n\right)$, а умножение на число$\alpha$ как $\alpha x =\left( \lfloor{\alpha }\rfloor x_1, \lfloor{\alpha}\rfloor x_2, ..., \lfloor{\alpha} \rfloor x_n\right)$, где $\lfloor{\alpha}\rfloor$ — целая часть числа.
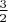
Ясное дело, что данное множество линейного пространства не образует, поскольку нарушается аксиома ассоциативности умножения на чило(в общем случае): $\left(\lfloor \alpha \beta \rfloor\right)\mathfrak{x} \ne \lfloor \alpha \rfloor \left(\lfloor \beta \rfloor \mathfrak{x}\right) $, что видно на примере $\frac{3}{2}$ и $2$, поскольку тогда, с одной стороны, $\left(\lfloor \frac{3}{2} \cdot 2\rfloor\right) \mathfrak{x} =3\mathfrak{x} $, а $\lfloor \frac{3}{2} \rfloor\left(\lfloor 2\rfloor\mathfrak{x} \right)=2\mathfrak{x} $.

Я же хотел доказать то же самое через наличие многих единичных элементов(кстати, счётно ли оно?..), так как каждый элемент $\lfloor a\rfloor$, где $a \geqslant 1$ и $a < 2$ будет единичным для данного пространства(я, кстати, путаю, судя по всему, ибо единичный элемент над полем, а не над пространством?), а их явно очень и очень много.

[ИСН]

В пространстве нет единичных элементов, так что и говорить о них незачем.

[мат-ламер]

tetroel в сообщении #874273 писал(а):

можно ли, если это так, на основании существования нескольких единичных элементов доказать

А в какой математической структуре может существовать несколько единичных элементов?

[ИСН]

В магме

[AV_77]

Там только односторонних единичных элементов может быть много, а двусторонний, если он есть, всегда единственный.

-- Ср июн 11, 2014 22:35:50 --

tetroel в сообщении #874287 писал(а):

Я же хотел доказать то же самое через наличие многих единичных элементов(кстати, счётно ли оно?..), так как каждый элемент $\lfloor a\rfloor$, где $a \geqslant 1$ и $a < 2$ будет единичным для данного пространства(я, кстати, путаю, судя по всему, ибо единичный элемент над полем, а не над пространством?), а их явно очень и очень много.

Вы сильно путаете терминологию. В векторном пространстве единичных элементов нет. Единичный элемент есть в поле, а при действии на векторы он играет роль тождественного оператора.

[arseniiv]

tetroel в сообщении #874287 писал(а):

Я же хотел доказать то же самое через наличие многих единичных элементов

Ваше доказательство простое и понятное — зачем что-то ещё?

Одна из аксиом линейного пространства (пускай его зовут $L$ над полем $F$), действительно, гласит, что $1_F\cdot x_L = x_L$, но нет нужды, чтобы $a_F\cdot x_L = x_L \Leftrightarrow a_F = 1_F$, так что такого и не требуют, и противоречия от равенства $\forall x_L\left(a_F\cdot x_L = x_L\right)$, если $a_F \ne 1_F$, вы не получите, и доказательства «нелинейности» $L$ потому тоже не получите.

[AV_77]

arseniiv в сообщении #874412 писал(а):

противоречия от равенства $\forall x_L\left(a_F\cdot x_L = x_L\right)$, если $a_F \ne 1_F$, вы не получите

Ну почему же, в этом случае аннулятор любого $x \in L$ отличен от нуля, а аннулятор является идеалом.