В общем, закончил я решать эту задачу. Поэкспериментировав, пришёл почти к той же идее, что предложил
_Ivana, а именно, требовать от аппроксимирующего полинома совпадения значений и производных на концах отрезка аппроксимации. Это удобно, потому что полиномы на соседних отрезках оказываются автоматически сшиты до нужной степени гладкости, и при оптимизации не нужно об этом дополнительно заботиться. Отличие моего подхода заключается в том, что я считаю излишним требовать совпадения второй производной аппроксимирующего полинома и аппроксимируемой функции на концах отрезка (во всяком случае, для моей задачи это не нужно). Вместо этого лучше потребовать минимума абсолютной величины невязки на отрезке аппроксимации. То есть четыре степени свободы съедаются жёсткими связями на граничные условия, а остающиеся две-три-четыре степени свободы можно использовать, чтобы получить наилучшее приближение. В моём случае это были полиномы пятой степени (шесть коэффициентов, двое из них свободны для оптимизации).
Область аргументов аппроксимируемой функции я разбил на десять участков. Для
![$x\in[2,+\infty]$ $x\in[2,+\infty]$](https://dxdy-01.korotkov.co.uk/f/0/f/d/0fdf4fcf2b6d1cd24bff8295a44ab26082.png)
я оставил одно слагаемое ряда и получил аппроксимирующую функцию

. Для
![$x\in[0,0.137]$ $x\in[0,0.137]$](https://dxdy-01.korotkov.co.uk/f/4/3/0/4309b4c67789721f225607411d8dc20f82.png)
я использовал аппроксимирующую функцию

, где

— полином второй степени, а

— константа. Отрезок
![$[0.137,2]$ $[0.137,2]$](https://dxdy-01.korotkov.co.uk/f/c/2/b/c2b5a36986dfac4b7a06bb6e7747aba682.png)
я разбил на 8 участков и в качестве аппроксимирующей функции на каждом из них использовал полиномы пятой степени

,

. Точки разбиения подбирал так, чтобы максимальная относительная невязка на каждом отрезке была одинакова. В результате с 10-ю участками и полиномами 5-ой степени удалось достичь точности

. Получилась такая приятная картинка:
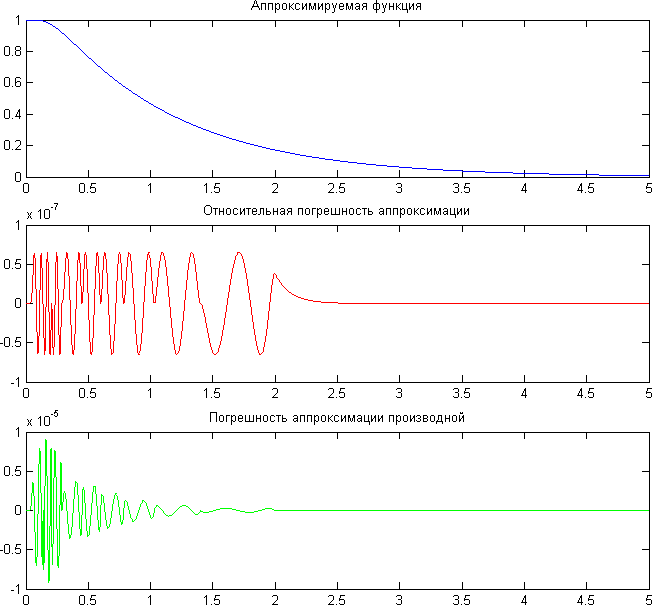
Абсолютная погрешность производной

, но для моей задачи это не страшно, тем более, что для
![$x\in[2,+\infty]$ $x\in[2,+\infty]$](https://dxdy-01.korotkov.co.uk/f/0/f/d/0fdf4fcf2b6d1cd24bff8295a44ab26082.png)
она существенно меньше.
Если кому-то будет интересно поиграться с аппроксимирующей функцией, прилагаю её скрипт для среды
MATLAB:
(heating_func.m)
Код:
function [y,yd1]=heating_func(x)
x=abs(x);
y=zeros(size(x));
yd1=zeros(size(x));
xsep=[
0.0000
0.1370
0.2064
0.2874
0.4504
0.6000
0.7848
1.0300
1.4008
2.0000
];
xmap=cell(10,1);
for k=1:9
xmap{k}=find(x>=xsep(k)&x<xsep(k+1));
end
xmap{10}=find(x>=xsep(10));
a=[
-5.750653895630414
3.683698706777679
-0.982526044380308
];
b=0.635465797673163;
xx=x(xmap{1});
tmp=exp(polyval(a,xx)-b./xx);
y(xmap{1})=1-tmp;
yd1(xmap{1})=-tmp.*(polyval(polyder(a),xx)+b./xx.^2);
yd1(x<0.01)=0.0;
a=[
-144.81809710607 -20.02894377021 5.21276060625 1.83719955731 0.41942048980 0.05885227953 0.00112746460 -0.00187990977
23.41159345255 -3.68258172789 -3.77654338415 -1.01861918246 -0.21268404753 -0.01442679345 0.01327728433 0.00970515107
2.52936486153 4.06168571317 1.65335453927 0.32966423792 -0.00488599537 -0.07103282584 -0.06203529702 -0.03874020251
-2.09004585638 -1.20123873791 -0.17319146490 0.22457590398 0.28480740793 0.25206599491 0.18851872527 0.11624746681
-0.34287831682 -0.59392381879 -0.74298932529 -0.71923092342 -0.62958500263 -0.51275921937 -0.37756394658 -0.23250597438
0.98529867349 0.94921049228 0.86512112038 0.74928343895 0.63626106124 0.51372345992 0.37762427873 0.23250678472
];
for k=2:9
xx=x(xmap{k})-0.5*(xsep(k)+xsep(k+1));
y(xmap{k})=polyval(a(:,k-1),xx);
yd1(xmap{k})=polyval(polyder(a(:,k-1)),xx);
end
y(xmap{10})=4/pi*exp(-x(xmap{10}));
yd1(xmap{10})=-4/pi*exp(-x(xmap{10}));
end
, если вас не затруднит, то буду очень благодарен, если вы проверите эту функцию на ваших данных.



