Есть задача, которая ставит в тупик, и другая, где я метод решения подобных не понял, видимо.
1. Найти все
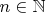
такие, что

делится на

.
Попытка решения в следующем. Я выясняю, что возможные

имеют вид

и только такие, ибо только тогда есть делимость левой части хотя бы на

.
Переход к нечетным основаниям:

затем

Легко видеть, что, по крайней мере, на

число делится бесспорно. Дальше что делать, пока не могу понять. Есть подозрение, что скобки могут разделиться на 5 не более одного раза каждая.
2. Даны

такие, что

. Найдите минимальное значение

.
Здесь я не могу понять, чего от меня хотят.
Из неравенства Коши получим

В то же время,
![$\frac{2(a+b+c)}{3} \geqslant \sqrt[3]{(a+b)(a+c)(b+c)}$ $\frac{2(a+b+c)}{3} \geqslant \sqrt[3]{(a+b)(a+c)(b+c)}$](https://dxdy-02.korotkov.co.uk/f/1/4/e/14ebe3bf2c2bde1ee462615855f1a72082.png)


Равенства достигаются при

, найдём

:


Так как

, то

.
Тогда

и

Мне сказали, что "равенство не гарантирует минимум". О чем речь?