Попробовал немножко поинтерполировать вашу функцию. При равномерном шаге
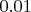
и интерполяции локальным кубическим сплайном Эрмита с оценкой производных в краях интервала по 7 точкам (по-русски говоря, на каждом интервале полином третьей степени, коэффициенты рассчитываются за несколько сложений/умножений, итоговый сплайн непрерывен и имеет непрерывную первую производную) ошибка интерполяции на интервале
![$[0, 0.5]$ $[0, 0.5]$](https://dxdy-02.korotkov.co.uk/f/1/c/2/1c28fc0c04e5b84e2db0db311a4f84a982.png)
не превышает

- при заданном шаге для этого интервала потребуется хранить массив всего 50 значений функции. При аргументе больше
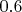
при таком шаге ошибка резко уменьшается, при аргументе большем

- до

и менее - можно выбрать более редкий шаг - существенно уменьшить массив хранимых значений.
При том же шаге и локальном сплайне Эрмита пятой степени (непрерывен сам сплайн и его первая и вторая производные, производные рассчитываются также по 7 точкам), ошибка на интервале
![$[0, 0.1]$ $[0, 0.1]$](https://dxdy-01.korotkov.co.uk/f/c/e/6/ce6525e7016dc7a2e88b1d894b2a015882.png)
не превышает

(нужны всего 10 значений функции), на
![$[0.1, 0.15]$ $[0.1, 0.15]$](https://dxdy-03.korotkov.co.uk/f/2/8/f/28f7a36626616e9b31270550a27f643d82.png)
не превышает

и далее порядок ошибки падает аналогично первому сплайну.

Если непонятно, могу написать формулы интерполяции данных сплайнов. Также можно легко скомбинировать эти сплайны с вашей найденной аппроксимацией в начальном интервале и вашим алгоритмом расчета хвоста.



