Здравствуйте!
Есть такая задачка: По формуле Стокса найти циркуляцию векторного поля

по контуру
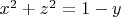
,

(первый октант).
Искомая циркуляция есть

Ротор поля

будет

Тогда

Единичная нормаль к поверхности
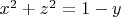
есть

Отсюда


Тогда

Справа двойной интеграл по области

, где

проекция поверхности

на плоскость

.
Подскажите, пожалуйста, я на верном пути? А то я запутался
