Порция 5.Перейдём к изучению бесконечных абелевых групп.
При этом, будем рассматривать группы по сложению.
Определение
-----------------
Абелева группа называется свободной если у неё есть базис и нет элементов конечного порядка, кроме нулевого

.
Базис может быть конечным или бесконечным, но мы пока не определили, что такое бесконечный базис, и этот случай рассматривать не будем.
Определение
------------------
Линейной комбинацией элементов

абелевой группы по сложению называется выражение

, где

- целые числа.
Определение
-----------------
Элементы

абелевой группы по-сложению называются линейно-независимыми, если из

следует

, для любых целых чисел

.
Лемма 1.20
---------------
Для того, чтобы элементы

были линейно-независимыми необходимо и достаточно, чтобы они были независимыми и не содержали элементов конечного порядка.
Доказательство:
----------------------
Пусть элементы

независимы и не содержат элементов конечного порядка.
Покажем, что они линейно-независимы.
Пусть

, где

- целые числа.
Поскольку элементы

независимы, то

.
Поскольку элементы

не имеют конечного порядка, то

.
Значит, элементы

линейно-независимы.
Что и требовалось
Пусть теперь элементы

линейно-независимы.
Покажем, что они независимы.
Пусть

, где

- целые числа.
Тогда

, следовательно

.
Значит, элементы

независимы.
Что и требовалось
Покажем, что

не содержат элементов конечного порядка.
Предположим обратное, и пусть элемент
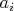
имеет конечный порядок

, где

- некоторый индекс.
Определим целые числа

следующим образом:

, а все остальные числа равны 0.
Тогда

и

, поскольку

.
Это противоречит тому, что элементы

линейно-независимы.
Что и требовалось.
Лемма 1.21
---------------
Пусть

- базис свободной абелевой группы

.
Тогда любые

элементов группы

линейно-зависимы.
Доказательство:
----------------------
Предположим, что это не так.
Пусть

- свободная абелева группа, для которой это не так, с наименьшим числом

элементов базиса.
Для
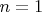
лемма верна, поскольку

, и если
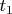
и

- различные целые числа, то хотя бы одно из них не равно нулю.
Поэтому

.
Пусть элементы

группы

линейно-независимы.
Тогда элементы

тоже линейно-независимы.
Пусть

, где

- целые числа, для

.
Если

для какого-то

, заменим

на

.
Без ограничения общности, предположим, что

.
Переставим эти целые неотрицательные числа в порядке убывания.
Если после этого, второе число не равно нулю, то отнимая его от первого числа можно уменьшить общую сумму чисел.
Повторяя эти действия, можно добиться того, чтобы все числа, кроме первого, были равны нулю.
Переставляя элементы

, заменяя

на

и повторяя эти действия, можно получить такие линейно-независимые элементы

, где

, что

, ...,

.
Пусть

- подгруппа группы

, генерированная элементами

.
Тогда

, и эти элементы линейно-зависимы, в силу минимальности

.
Что противоречит линейной независимости элементов

.
Из доказанной леммы следует, что все базисы свободной абелевой группы имеют одинаковое количество элементов.
Определение
-----------------
Рангом свободной абелевой группы называется количество элементов в её базисе.
Лемма 1.22
---------------
Пусть

- свободная абелева группа ранга

.
Пусть

, ...,
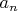
- базис группы

.
Любая нетривиальная подгруппа

группы

является свободной абелевой группой ранга

.
Более того, существует такой базис

подгруппы

(где

), что

является линейной комбинацией элементов

для любого

.
Доказательство:
-------------------------
Если
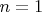
, то

генерируется элементом

, где

- наименьшее целое положительное число, для которого

.
Предположим, что лемма верна для ранга

и докажем, что она верна для ранга

.
Пусть

- наименьшее целое положительное число, такое, что

, где

- целые числа.
Если такого

не существует, то

является подгруппой свободной абелевой группы с базисом
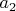
, ...,
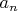
и лемма верна согласно предположению индукции (если

является линейной комбинацией элементов

, то

является линейной комбинацией элементов

, для любого

).
Пусть

- какой-либо элемент подгруппы

этого вида.
Любой элемент подгруппы

имеет вид

, где

- целое число, и

- целые числа.
Пусть

- подгруппа генерируемая элементами

вида

.
Если

тривиальна, то

генерируется элементом

, поскольку

для любого

.
Пусть

- нетривиальна.
Поскольку

является подгруппой свободной абелевой группы, генерированной элементами

, то согласно предположению индукции,

имеет базис

, ...,

, удовлетворяющий условиям леммы, где

.
Элементы

- линейно-независимы, так как если

, то

в силу линейной независимости элементов

, значит

и

, значит

, ...,

в силу линейной независимости элементов

.
Элементы

генерируют подруппу

, поскольку

для любого

, а элементы

генерируют подруппу

.
Поскольку элементы

линейно-независимы и генерируют подруппу

, то они образуют её базис.
Определение
-----------------
Абелева группа называется конечно-генерированной, если она генерируется конечным числом элементов.
Теорема 1.23
-----------------
Пусть

- конечно-генерированная абелева группа, не имеющая элементов конечного порядка, кроме нуля

.
Тогда

является свободной абелевой группой с конечным базисом.
Доказательство
------------------------
Пусть элементы

, ...,

- генераторы группы

.
Пусть

- наибольшее колличество линейно-независимых элементов, которые можно выбрать в

.
Пусть

, ...,
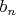
- линейно-независимые элементы, выбранные в

.
Пусть

- подгруппа группы

, генерируемая элементами

.
Тогда

- базис подгруппы

, а поскольку в ней нет элементов конечного порядка, кроме

, то

- свободная абелева группа.
Ввиду максимальности

, для любого

элементы

,

, ...,
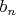
- линейно-зависимы, следовательно

для некоторого целого положительного числа

.
Пусть

- наименьшее общее кратное чисел

, ...,

.
Тогда для любого

.
Пусть

- множество всех элементов группы

, представимых в виде

, где

.
Тогда

.
Множество

является подгруппой группы

, поскольку если

и

, то

.
Поскольку

- свободная абелева группа с конечным базисом и

- подгруппа группы

, то согласно лемме 1.22, подгруппа

тоже является свободной абелевой группой с конечным базисом.
Пусть

- базис группы

, где

.
Элементы

линейно-независимы, так как если

, где

- целые числа, то

, следовательно

.
Для любого

принадлежит

и является линейной комбинацией элементов базиса

.
Значит, для любого

, где

является линейной комбинацией элементов

.
Из

следует

, следовательно

, следовательно

, где предпоследнее равенство выполняется ввиду отсутствия элементов конечного порядка, кроме

.
Значит

генерируют группу

.
Поскольку элементы

линейно-независимы и генерируют группу

, то

- базис группы

.
Таким образом группа

, не имеющая элементов конечного порядка, имеет конечный базис.
Значит группа

- свободная абелева группа с конечным базисом.
Теорема 1.24
------------------
Пусть

- конечно-генерированная абелева группа, и

- подгруппа её элементов конечного порядка.
Тогда

- конечная группа.
Если подгруппа

не совпадает с группой

, то группа

является прямой суммой некоторой своей подгруппы

и

.
При этом, подгруппа

является свободной абелевой группой.
Доказательство:
----------------------
Покажем, что

- конечно-генерированная абелева группа.
Если

совпадает с

, то это верно.
Пусть

не совпадает с

.
Фактор-группа

является конечно-генерированной абелевой группой, поскольку такой является группа

.
Если элемент

не принадлежит

, то

не принадлежит

, где

- любое целое число, отличное от нуля.
Поэтому фактор-группа

не имеет элементов конечного порядка, кроме

.
Значит, фактор-группа

является конечно-генерированной абелевой группой, не имеющей элементов конечного порядка, кроме

.
Согласно теореме 1.23,

является свободной абелевой группой с конечным базисом.
Пусть

, ...,

- базис фактор-группы

.
Пусть

- подгруппа группы

генерируемая элементами

, ...,
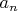
.
Тогда

не имеет с

общих элементов, кроме

.
В самом деле, если

, где

- целые числа, то

, следовательно

, значит
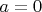
.
Из этого следует, что в группе

нет элементов конечного порядка, кроме

.
Элементы

линейно-независимы.
В самом деле, если

, где

- целые числа, то

, следовательно

.
Поскольку элементы

линейно-независимы и генерируют подгруппу

, то они образуют её базис.
Значит подгруппа

имеет конечный базис и не имеет элементов конечного порядка, кроме

.
Следовательно,

- свободная абелева группа.
Группа

является суммой подгрупп

и

, поскольку любой элемент фактор-группы

равен

, где

.
Поскольку подгруппы

и

не имеют общих элементов, кроме

, то группа

является прямой суммой подгрупп

и

, в силу теоремы 1.12.
Любой из конечного числа генераторов группы

представим в виде суммы элемента из

и элемента из

.
Пусть

- генераторы группы

, где

, а

.
Покажем, что элементы

генерируют группу

.
Для любого


, где

- целые числа.
Значит,

.
Поскольку

, и подгруппы

и

не имеют общих элементов, кроме

, то

.
Значит для любого

, где

- целые числа.
Что и требовалось.
Значит,

- конечно-генерированная абелева группа.
Поскольку генераторы группы

имеют конечный порядок, то

- конечная группа.



