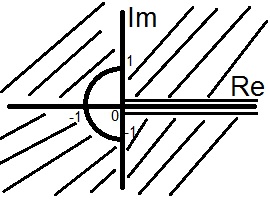
Задание: конформно отобразить комплексную плоскость с выкинутым единичным полукругом и разрезом от нуля до бесконечности по положительной части действительной оси на единичный круг.
в арсенале:
принцип симметрии
показательная/логарифмическая функции
функция Жуковского/обратная ей
дробно-линейная
степенная
и прочие сдвиги, повороты и сжатия/расширения
как ни крутил, ничего не получается, пытался начать с принципа симметрии, в качестве кривой, относительно которой берутся симметричные области, брал действительную ось. После чего применял функцию Жуковского, там получалась плоскость с выкинутым квадрантом и разрезом. Далее тупик.
Иначе, пробовал после принципа симметрии применить логарифмическую функцию, получил полосу и полуполосу, из которых смог с помощью дробно-лин. перейти в комплексную плоскость, с выкинутыми полукругами разных радиусов, но тоже тупиковая ситуация.
Прошу подсказать, как ещё можно попробовать?