Пусть

- группа,

. Следует ли из этого, что центр

тривиален и все автоморфизмы внутренние?
Пусть

- изоморфизм,

.
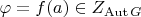
.

коммутирует со всеми автоморфизмами, например, со внутренними:
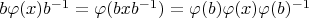
. Сопряжения элементами

и

совпадают,

.
Это можно доказать, зная лишь определения? Каких-либо нужных теорем могу не знать, т.к. занимаюсь самостоятельно.