Здравствуйте, уважаемые участники форума. Помогите, пожалуйста, разобраться с такой задачей.
Дано, что функция
![$f: R \rightarrow [0;+\infty]$ $f: R \rightarrow [0;+\infty]$](https://dxdy-01.korotkov.co.uk/f/0/e/1/0e1e7876dc76469909a53b051dcf82a682.png)
- выпуклая вниз. Доказать, что функция:

также выпуклая вниз.
Хочу показать, что

для любых

.


И тогда

и из условия выпуклости функции

:


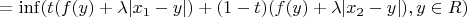
Можно ли теперь утвержать, что последний

равен сумме

и

? Если нет, тогда как в таком случае рассуждать? Заранее благодарен.