Человек стоит на диске, который вначале неподвижен, но может вращаться относительно вертикальной оси, проходящей через его центр. Момент инерции диска с человеком

. В руках человек держит колесо, ось которого вертикальна и расположена на расстоянии

от центра диска.
Колесо вращается, делая

. Определить угловую скорость вращения диска

, если человек повернет ось колеса на 180°. Масса колеса m=3 кг.
В условии задачи не дан радиус колеса

. Будем считать, что он известен, так как без него условий не достаточно.
Мое решение:
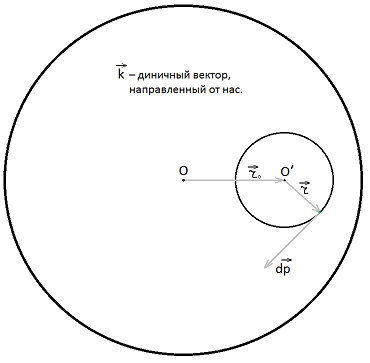
Итак, в начале платформа неподвижна. Момент импульса колеса относительно оси вращения платформы

, вращающегося вокруг собственной оси вращения

, равен
![$\vec{M_O}=\sum \left[\vec{r_0}+\vec{r},\, d\vec{p}\,\right]=\sum \left[\vec{r_0},\, d\vec{p}\,\right]+\sum \left[\vec{r},\, d\vec{p}\,\right]=0+mr^2\omega\vec{k}$ $\vec{M_O}=\sum \left[\vec{r_0}+\vec{r},\, d\vec{p}\,\right]=\sum \left[\vec{r_0},\, d\vec{p}\,\right]+\sum \left[\vec{r},\, d\vec{p}\,\right]=0+mr^2\omega\vec{k}$](https://dxdy-04.korotkov.co.uk/f/7/a/4/7a48e1c8de0a64f065fa3d6d8de4723c82.png)
.
То есть получается, что моменты импульса вращающегося колеса на неподвижной платформе относительно осей

и

равны. Это правильно?
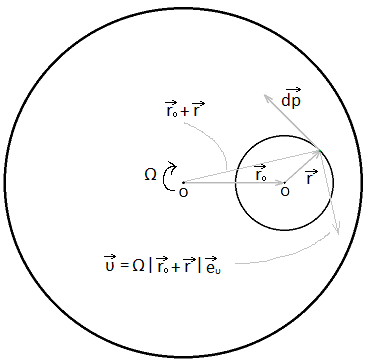
Далее ось вращения колеса повернули на 180°.
![$\vec{M'_O}=I\Omega\vec{k} +\sum \left[\vec{r_0}+\vec{r},\, \left(\vec{v}+\Omega\left|\vec{r_0}+\vec{r}\,\right|\vec{e_v}\right)dm\right]=I\Omega\vec{k} +\sum \left[\vec{r_0}+\vec{r},\, \vec{v}dm\,\right]+\\+\Omega\sum \left|\vec{r_0}+\vec{r}\,\right|dm\left[\vec{r_0}+\vec{r},\, \vec{e_v}\,\right]=\\=I\Omega\vec{k}-mr^2\omega\vec{k}+\Omega\sum \left|\vec{r_0}+\vec{r}\,\right|dm\left|\vec{r_0}+\vec{r}\,\right|\vec{k}=I\Omega\vec{k}-mr^2\omega\vec{k}+\vec{k}\Omega\int\limits_{0}^{2\pi r}(r^2+2rr_0\cos\alpha+r_0^2)\frac{m}{2\pi r}dl=I\Omega\vec{k}-mr^2\omega\vec{k}+\Omega m(r^2+r_0^2)\vec{k}.$ $\vec{M'_O}=I\Omega\vec{k} +\sum \left[\vec{r_0}+\vec{r},\, \left(\vec{v}+\Omega\left|\vec{r_0}+\vec{r}\,\right|\vec{e_v}\right)dm\right]=I\Omega\vec{k} +\sum \left[\vec{r_0}+\vec{r},\, \vec{v}dm\,\right]+\\+\Omega\sum \left|\vec{r_0}+\vec{r}\,\right|dm\left[\vec{r_0}+\vec{r},\, \vec{e_v}\,\right]=\\=I\Omega\vec{k}-mr^2\omega\vec{k}+\Omega\sum \left|\vec{r_0}+\vec{r}\,\right|dm\left|\vec{r_0}+\vec{r}\,\right|\vec{k}=I\Omega\vec{k}-mr^2\omega\vec{k}+\vec{k}\Omega\int\limits_{0}^{2\pi r}(r^2+2rr_0\cos\alpha+r_0^2)\frac{m}{2\pi r}dl=I\Omega\vec{k}-mr^2\omega\vec{k}+\Omega m(r^2+r_0^2)\vec{k}.$](https://dxdy-03.korotkov.co.uk/f/2/e/2/2e21282405a8b53b7ec612cdb993e84882.png)

– закон сохранения момента импульса.



Все верно?