Новые формулы полного решения уравнения Пифагора

[Alfigor]

НОВЫЕ ФОРМУЛЫ ПОЛНОГО РЕШЕНИЯ УРАВНЕНИЯ ПИФАГОРА

Получены формулы (5), возможно ранее неизвестные, полного решения уравнения Пифагора

$$ x^2 + y^2 = z^2\qquad\eqno(1).$$

Формулы отличаются от известных уже около 3000 лет формул полного решения древних индусов и вавилонян (2) и в широкодоступной литературе нигде
не встречаются, встречаются только формулы (2). Список литературы [1 - 10] приведен в конце сообщения.
Формулы древних индусов:

$$x= a^2 - b^2;\quad y=2ab;\quad z= a^2 + b^2,\text{ где } a > b\quad\eqno(2).$$

Уравнение (1) имеет целые решения – общеизвестные тройки чисел Пифагора. Таких решений, как доказал ещё Евклид, имеется бесконечное множество. Тройку целых положительных чисел $x, y, z$, не имеющих общих делителей, назовём оригинальным решением уравнения (1). Далее оригинальные решения будут обозначаться большими буквами $X,Y,Z$. Для упорядочения пусть далее везде $x < y < z$ и $X < Y < Z$.
Если $x, y, z$ - целые положительные числа, то существуют целые положительные числа $a$ и $b$, такие, что

$$ x = z - a\quad \text{ и } \quad y = z - b,$$

где $b < a$, так как $x < y$. Тогда уравнение (1) запишется следующим образом:

$$(z - a)^2 + (z - b)^2 = z^2\eqno(3).$$

После возведения в степень и группирования из (3) получится следующее уравнение:

$$z^2 - 2(a + b) z + a^2 + b^2 =0\eqno(4).$$

В результате решения уравнения (4) относительно $z$ получим новые формулы полного решения уравнения (1):

$$x=\sqrt{2ab}+b;\quad y = \sqrt{2ab} + a;\quad z = \sqrt{2ab} + a + b;\eqno(5).$$

Здесь корень $\sqrt{2ab}$ не может быть отрицательным, если $x, y, z$ – натуральные числа.

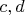
Число $\sqrt{2ab}$ является целым в следующих случаях ($c, d$ – любые взаимно простые числа, по крайней мере, одно из них – нечётное):

- случай 1: $a=2c^2, b=d^2, \sqrt{2ab}=2cd;$ после подстановки в (5) значений $a$ и $b$ получим:

$$X=d(2c+d);\quad Y=2c(c+d);\quad Z=2c(c+d)+d^2;\eqno(6),$$

здесь $a > b; a, Y$ – чётные; $b, X, Z$ – нечётные числа;

- случай 2: $a=c^2, b=2d^2, \sqrt{2ab}=2cd;$ после подстановки в (5) значений $a$ и $b$ получим:

$$X=2d (c+d);\quad Y=c(c+2d);\quad Z=c(c+2d)+2d^2;\eqno(7),$$

здесь $a > b; a, Y, Z$ – нечётные; $b, X$ – чётные числа.

Ниже приведён пример получения последовательностей троек решений уравнения (1), не имеющих общих делителей, с помощью новых формул полного решения. При этом всегда должно быть $a > b$ и $a, b$ должны быть взаимно просты. Последовательности решений названы по значению числа $m$, см. ниже (8, 9), например, если $m=1$, то последовательность П1 (Пифагор).

Последовательность П1: $b=d^2=1^2; a=2c^2; \sqrt{2ab}=2c$, где $c=1,2,3,…$
Подставив $d=1$ и $c$ в (6), получим формулы для неограниченной последовательности оригинальных решений: $X = 2c+1; Y = 2c(c+1); Z = Y+1.$
3,4,5; 5,12,13; 7,24,25; 9,40,41; 11,60,61; 13,84,85; 15,112,113; 17,144,145; …

Последовательность П2: $b=2d^2=2\cdot1^2; a=c^2; \sqrt{2ab}=2c^2$ , где $c=3,5,7,…$
После подстановки $d=1$ и $c$ в (7): X = 2(c+1); Y = c(c+2); Z = Y +2.$
8,15,17; 12,35,37; 16,63,65; 20,99,101; 24,143,145; 28,195,197; 32,255,257; …

П3: $X=3(2c+3); Y=2c(c+3); Z=Y+9,$ где $ c\bmod3 \ne 0$, $c=4,5,7,8,10,11…$
33,56,65; 39,80,89; 51,140,149; 57,176,185; 69,260,269; 75,308,317; 87,416,425;...
П4: $X=4(c+2); Y=c(c+4); Z=Y+8,$ где $c=3,5,7,…$
20,21,29; 28,45,53; 36,77,85; 44,117,125; 52,165,173; 60,221,229; 68,285,293; …
П5, П6, П7 ... и т.д.

В более удобном для получения этих последовательностей виде формулы (6, 7) будут выглядеть следующим образом:
$\cdot$ $m$ - нечетное, $c$ - четное/нечетное:

$$X=m(2c+m);\quad Y=2c(c+m);\quad Z=Y+m^2;\eqno(8),$$

$\cdot$ $m$ - четное, $c$ - нечетное:

$$X=m(2c+m/2);\quad Y=c(c+m);\quad Z=Y+m^2 /2;\eqno(9),$$

где $c=g+i, i=0,1,2,3,… $, но $ c \mod m \ne0$, кроме $m=1$; начальное значение $g$ числа $c$ равно $g=\lceil(m/\sqrt{2})\rceil$, если $ g \mod m =0$, то $g=g+1$.
Формулы (8, 9) работают при любых значениях чисел $m\text{ и }c$, но для получения оригинальных решений необходимо придерживаться данных здесь условий для значений числа $c$.

С помощью формул (2) теорема Ферма доказана для $n=4$ и для всех $n$ кратных 4 методом Ферма [2][4], т.е. методом бесконечного спуска, а с помощью новых формул (5) доказывается тем же методом для всех нечетных степеней $n\geqslant3$.

Доказательство для $n=3$ будет дано в следующем сообщении.

Литература:
1. Диофант Александрийский «Арифметика и книга о многоугольных числах», М: Наука, 1974.
2. Хинчин А.Я. «Великая теорема Ферма» », М.: ЛКИ, 2007.
3. Берман Г.Н. «Число и наука о нём», М.: ЛКИ, 2007.
4. Постников М.М. «Теорема Ферма» », М.: Наука, 1978.
5. Курант Р., Роббинс Г., «Что такое математика?», М.:МЦНМО, 2000.
6. Оре О. «Приглашение в теорию чисел», М: Наука, 1980.
7. В. А. Никифоровский, «Из истории алгебры XVI-XVII вв.», М.: Наука, 1979.
8. З.И. Боревич, И.Р. Шафаревич «Теория чисел», М.: Наука, 1985.
9. Ю. И. Манин, А. А. Панчишкин, “Введение в современную теорию чисел”, М.: МЦНМО, 2009.
10. Г.Корн, Т.Корн, «Справочник по математике», М.: Наука, 1977.

[vasili]

Уважаемый Alfidor! Вы обозначили числа в равенствах (2) и равенствах (3) одними буквами a и b.
Но это не так для фиксированного решения уравнения (1). Пример решение (1): $X = 5$ ,$Y =12$, $Z =13$ в этом случае
a =3, b =2.
Но $X= Z- a =13-3 = 10$,
$Y = Z -b = 13-2 = 11$.
Числа 10,11 и 13 не являются решением (1).
Если $X = Z -a_1 = 13 - 8$, отсюда $ a_1 =8$
$Y =Z -b_1 = 13 -1$, отсюда $b_1 = 1$
Тогда все верно
$X = (2a_1b_1)^1/2 + b_1 = (16)^1/2 +1 = 5$
$Y = (16)^1/2 + 8 = 12$
$Z =(16)^1/2 + 1 +8 = 13$.

[Kudov]

Все это прекрасно, но по этой методике невозможно определить в какую пифагорову тройку входит заданное число.