Вычеты

[Munin]

Brukvalub в сообщении #863073 писал(а):

Бред какой-то. "Новооткрывателю" полезно узнать. что ротор - это исключительно "трехмерная операция"

исключительно потому, что для других размерностей он так не называется. А так, для любой размерности $n$ есть операция внешнего дифференцирования дифференциальной $k$-формы для любого $k,$ которая для 1-формы (ковектора) даёт 2-форму (и для $k$-формы - $k+1$-форму). Эта операция в размерности 3 даёт ротор (при наличии метрики и формы объёма, которые в евклидовом случае доступны), а в размерности 2 даёт скалярную плотность (или скаляр, при наличии формы объёма, которая в случае комплексной плоскости тоже доступна).

И формула $\dfrac{\partial v_y}{\partial x}-\dfrac{\partial v_x}{\partial y}$ здесь работает ничем не хуже, чем в трёхмерном случае - для $z$-компоненты ротора, в том числе для векторного поля, не имеющего $z$-компоненты.

Brukvalub в сообщении #863073 писал(а):

Перед изобретением велосипеда сильно полезно ознакомиться с уже имеющимися конструкциями и не смешить ученый люд. :D

Тут можно поменьше смеяться, и побольше радоваться тому, что принцип велосипеда ухвачен верно, и можно подкидывать для знакомства те самые уже имеющеся конструкции.

Математика едина, и именно по математической сути ТС перешёл от одного к другому, а разные термины здесь возводят ложные границы, которых на самом деле нет.

[Munin]

Вспомнил! Sicker уже сталкивался с этими вещами в «Re: Внешний дифференциал» (Munin) .

Итак, напомню,

def

Munin в сообщении #859254 писал(а):

внешняя производная - это когда к тензору $T_{ij\ldots p}$ (нужным образом антисимметричному) приписывают ещё дифференцирование, и всё это опять антисимметризуют: $\partial_{[q}T_{ij\ldots p]}.$

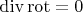
Внешняя производная в обозначениях дифференциальных форм записывается как $d\omega,$ где $\omega$ - дифференцируемая форма, а $d$ - оператор. В частности, $dd=0.$ Это свойство - обобщение таких свойств, как $\operatorname{div}\operatorname{rot}=0$ и $\operatorname{rot}\operatorname{grad}=0.$

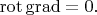
Векторы обычного векторного исчисления могут ставиться в соответствие как 1-формам, так и $n-1$-формам, в зависимости от контекста (и существует операция сопряжения Ходжа ("звёздочка Ходжа"), которая меняет ранг тензора с $k$ на $n-k$ - нормированная свёртка с тензором Леви-Чивиты). Скаляры - либо 0-формам (скаляр), либо $n$-формам (скалярная плотность).

def

Обратная операция (нахождение такой формы, внешняя производная от которой равна заданной) называется внешней антипроизводной. Она не однозначна, но об этом ниже.

def

Существует интеграл (определённый) от $k$-формы по $k$-мерной поверхности в $n$-мерном пространстве. В тензорных обозначениях он выглядит как $\int\limits_{M} T_{ij\ldots p}(dx^{[i}dx^{j}\ldots dx^{p]}),$ и всегда даёт в результате скаляр. Поверхность должна быть ориентируемой. В обозначениях дифференциальных форм это записывается как $\int\limits_{M}\omega$ - именно так, "без дифференциала".

def

Для $k$-мерной ориентируемой поверхности с краем существует операция взятия границы, которая даёт $k-1$-мерную ориентируемую поверхность. Обозначается $\partial M,$ где $\partial$ - оператор. Из топологии вытекает, что граница не имеет собственной границы, то есть $\partial\partial=0.$

theorem

Выполняется обобщённая теорема Стокса: $\int\limits_{M}d\omega=\int\limits_{\partial M}\omega.$ Она включает в себя 1-мерную теорему Ньютона-Лейбница (и её $n$-мерные обобщения для интеграла по линии), 2-мерную теорему Грина, 3-мерную теорему Стокса (и её $n$-мерные обобщения для интеграла по двумерной поверхности с краем), 3-мерную теорему Гаусса (и её $n$-мерные обобщения для интеграла по $n$-мерному объёму).

def

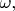
• Замкнутой формой называется такая форма $\omega,$ что $d\omega=0.$
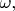
• Точной формой называется такая форма $\omega,$ что существует такая форма $\lambda,$ что $d\lambda=\omega.$
Эти понятия лучше всего осваивать, сравнивая их с разновидностями скалярных и векторных полей на плоскости и в пространстве.

def start

Точные формы - всегда замкнутые, поскольку $d(d\lambda)=(dd)\lambda=0.$ Но обратное, вообще говоря, неверно. Зато, обратное верно, если область, в которой рассматривается форма, $k$-связна, где $k$ - степень формы $\omega.$ $k$-связность означает, что любое вложение $k$-мерной сферы можно стянуть в точку. Например, 0-связность (также называемая просто "связность") означает, что любую пару точек можно стянуть в одну точку - область не состоит из раздельных "кусков". 1-связность означает, что любую петлю можно стянуть в одну точку. 2-связность - что любой "двумерный пузырь" можно стянуть в одну точку, и так далее. Если область не $k$-связна, то в ней есть какие-то топологические препятствия для стягивания, размерности не меньше $n-k-1.$ Например, область на плоскости будет не 1-связна, если в ней выколоть точку. Но 3-мерная область будет не 1-связна, если в ней выколоть не меньше чем линию (замкнутую в петлю, или уходящую в границы области или на бесконечность). Если в 3-мерной области выколоть точку, то такая область будет не 2-связна, но 1-связна и 0-связна.

Итак, если область $k$-связна, то замкнутые формы равны точным. Но если область не $k$-связна, то у замкнутых форм появляются ещё дополнительные "степени свободы". Например, векторное поле - замкнутая форма, если его $\operatorname{rot}\mathbf{v}=0,$ такое поле называется безвихревым. Но оно будет точной формой, $\mathbf{v}=\operatorname{grad}\varphi,$ потенциальным полем, только если область 1-связна. Это значит, что любую петлю можно стянуть в точку. Рассмотрим интеграл по такой петле: он существует и скалярный, на векторном языке он называется циркуляцией. Безвихревое поле имеет циркуляцию, равную нулю, на любом стягиваемом контуре, в силу теоремы Стокса (обычной). Но если контур нестягиваемый, и охватывает какое-то препятствие (например, выколотую точку на плоскости, или выколотую линию в 3-мерии), то теорему Стокса применить нельзя, и циркуляция может быть не равна нулю. Зато, такая циркуляция будет постоянна для любых контуров, охватывающих это препятствие. Для нескольких препятствий будет своя циркуляция для каждого по отдельности.

На алгебраическом языке, это формулируется так: множество всех точных форм данной степени является группой по сложению (поскольку их можно складывать и вычитать между собой), множество всех замкнутых форм также является группой, и можно взять факторгруппу замкнутых форм по точным $C_k/E_k.$ Алгебраический смысл факторгруппы в том, что две точные формы отличаются между собой на точную форму, а две замкнутые формы - могут отличаться между собой на точную, или на замкнутую. Все замкнутые формы разбиваются на классы, внутри каждого из которых отличаются между собой только на точную. Такие классы тоже можно рассматривать как группу по сложению, если выбрать в каждом классе представителя, и складывать их. Такие представители будут образовывать очень простую алгебраическую структуру, их множество будет подобно множеству всех возможных значений циркуляции.

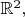
Эта факторгруппа называется группой когомологий (здесь: когомологий де Рама). Группа когомологий - возникает из топологических свойств данной области, и не зависит от конкретных форм. Величины циркуляций, и их аналогов, принимают значения в этой группе. Например, если в области есть одно препятствие, то эта группа - действительные числа, а если два препятствия - то $\mathbb{R}^2,$ поскольку для каждого препятствия может быть задана своя циркуляция.

def end

Как-то "галопом по Европам" получилось. Для дальнейшего чтения:
- внешние формы и дифференциальные формы (встречаются в учебниках алгебры и матанализа);
- дифференциальная геометрия (более подробно аппарат дифференциальных форм, операций интегрирования и дифференцирования);
- дифференциальная и алгебраическая топология (гомологии и когомологии, интегрирование с точки зрения коцепей и когомологий).

[Sicker]

Munin, спасибо большое)
Правда новое я узнал только от def start до def end

[Munin]

Это и хорошо.

[Brukvalub]

Munin в сообщении #863096 писал(а):

Brukvalub в сообщении #863073 писал(а):

Бред какой-то. "Новооткрывателю" полезно узнать. что ротор - это исключительно "трехмерная операция"

исключительно потому, что для других размерностей он так не называется. А так, для любой размерности $n$ есть операция внешнего дифференцирования дифференциальной $k$-формы для любого $k,$ которая для 1-формы (ковектора) даёт 2-форму (и для $k$-формы - $k+1$-форму). Эта операция в размерности 3 даёт ротор (при наличии метрики и формы объёма, которые в евклидовом случае доступны), а в размерности 2 даёт скалярную плотность (или скаляр, при наличии формы объёма, которая в случае комплексной плоскости тоже доступна).
...

Я из-за отсутствия экстрасенсорных особенностей форму-то и не разглядел, а увидел плоское векторное поле. К тому же, не считаю нужным поощрять дилетантские потуги совершать с помощью форума "открытия" в корявом виде того, что давно открыто и ясно написано в учебниках. Такие "открытия" - не доблесть, а умовредительство.

[Munin]

Brukvalub в сообщении #863286 писал(а):

Я из-за отсутствия экстрасенсорных особенностей форму-то и не разглядел, а увидел плоское векторное поле.

Ну, бывает.

Brukvalub в сообщении #863286 писал(а):

К тому же, не считаю нужным поощрять дилетантские потуги совершать с помощью форума "открытия" в корявом виде того, что давно открыто и ясно написано в учебниках.

Где вы увидели "с помощью форума"? Человек сначала дотумкал до чего-то сам, потом пришёл на форум, и тут его наставили на путь истинный. По-моему, всё гармонично.