Первообразная.

[Katmandu]

Расскажите пожалуйста, что такое первообразная, а то я уже второй год учусь в университете, а понять не могу. help

[ewert]

(Оффтоп)

Katmandu в сообщении #858726 писал(а):

Расскажите пожалуйста, что такое первообразная, а то я уже второй год учусь в университете, а понять не могу.

Тогда лучше на третий год пойти в армию; ну а уж на четвёртый -- как выйдет.

[Vova_Gidro]

(Оффтоп)

ewert в сообщении #858729 писал(а):

Тогда лучше на третий год пойти в армию; ну а уж на четвёртый -- как выйдет.

А на четвертый в школу:)

По теме для Katmandu. Первообразной для функции $f(x)$ называется такая функция $F(x)$, что $F'(x)=f(x)$. Множество всех первообразных для функции $f(x)$ называют неопределенным интегралом от $f(x)$.
А что конкретно вам непонятно?

[Katmandu]

ewert в сообщении #858729 писал(а):

Тогда лучше на третий год пойти в армию

Я уже был в армии, там мне голову отбили, теперь плохо понимаю простые вещи.

[Munin]

Хорошо, а что такое образ и прообраз вы понимаете?

Вот есть некоторое отображение $m\colon X\to Y.$ И для некоторого $x\in X$ существует $m(x),$ а для некоторого $y\in Y$ существует $m^{-1}(y).$

[Katmandu]

$m(x)$ это функция заданная на $X$.. когда подставим все $x$ получим множество $Y$, $m^{-1}(y)$ обратная функция, когда подставим все $y \in Y$ получим множество $X$
Я так это понимаю

[Munin]

Katmandu в сообщении #858774 писал(а):

:? $m(x)$ это функция заданная на $X$.. когда подставим все $x$ получим множество $Y$

Не обязательно. Получим некое множество $m(X),$ такое что $m(X)\subseteq Y.$ Если бы мы получили $m(X)=Y,$ то $m$ называлось бы сюръективным отображением ("отображением на"). Ну да ладно.

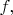
Рассмотрим множество функций. На нём определено отображение (не на всех функциях, но пока опустим эту деталь), которое называется дифференцированием, $D[f]=f'.$ Так вот, $D[f]=f'$ называется производной от функции $f,$ а наоборот, $D^{-1}[f]$ - взятие первообразной, и $g\in D^{-1}[f]$ - первообразная.

Вот и всё, больше ничего в этом понятии нет.

-- 04.05.2014 11:46:08 --

Чёрт. Чё-то я не читатель сегодня. Vova_Gidro же уже всё объяснил.

[Katmandu]

Множество каких функций нужно рассмотреть? непрерывных?

[Munin]

Пренебрегая подробностями, $Y$ - множество непрерывных функций, а $X$ - множество непрерывных функций, имеющих непрерывную первую производную (такие функции называются гладкими функциями).

[arseniiv]

А можно вообще всех (и даже беря функции из, скажем, $\{2,3\}$ в $\mathbb Z$). Некоторые не будут иметь производную и не подойдут поэтому, некоторые будут иметь не ту производную и не подойдут поэтому.

[Nirowulf]

(Оффтоп)

Katmandu в сообщении #858726 писал(а):

а то я уже второй год учусь в университете

Katmandu писал(а):

Род занятий: Школьник 11 класс

Does not compute=)