Мне кажется, надо попытаться продвинуться как можно дальше, не прибегая к координатам. В векторном виде соотношения проще.
Итак, угол

между

и

постоянный (естественно, мы используем натуральную параметризацию).

Упрощаем. Во-первых,


, или

Во-вторых, используем


Я домножаю обе части на 2 (это подсказка).

Вы можете упростить левую часть?
-- Вт апр 15, 2014 00:49:08 --Интеграл от полной производной по замкнутому пути равен нулю.
Не могу удержаться, чтобы не привести иллюстрацию. Вы путешествуете по горам неделю и
возвращаетесь в исходную точку. Если за понедельник Вы поднялись на
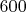
м, за вторник на

, за среду на

, за четверг на

, и так далее до воскресенья, то сумма всех этих чисел будет равна нулю. Потому что Вы интегрировали производную от высоты по замкнутому пути.



