Про своиство умноженных матриц

[ghetto]

Пусть $1 \le r \le m$ and $1 \le s \le m$.

Пусть

$$ I_{rs} = \begin{pmatrix} 0 & \ldots & 0 & \ldots & 0\\ \vdots & &&& \vdots\\ 0 & \ldots & 1_{rs} & \ldots & 0 \\ \vdots & &&& \vdots \\ 0 & \ldots & 0 &\ldots & 0 \\ \end{pmatrix} $$

$$ A = \begin{pmatrix} a_{11} & \ldots & a_{1n}\\ \vdots & &\vdots\\ a_{m1} & \ldots & 1_{mn} \\ \end{pmatrix} $$

1. Что такое $I_{rs}A$?

2. Пусть $r \neq s$. Что такое $ \left (I_{rs} + I_{sr} \right)A$ ?

1. $I_{rs}A$ есть матрица чей ряд $r$ скопирован с ряда $s$ матрицы $A$. Все ее остальные компоненты равны нулю.

2. Имеет ли смысл $I_{rs} + I_{sr}$? Как можно слагать матрицы с разным кол-вом рядов и коллон? Плиз, обьясните.

[patzer2097]

ghetto в сообщении #847299 писал(а):

2. Имеет ли смысл $I_{rs} + I_{sr}$? Как можно слагать матрицы с разным кол-вом рядов и коллон?

почему с разным, и то и другое - квадратные матрицы порядка $m$ в Вашем случае

[ghetto]

patzer2097 в сообщении #847300 писал(а):

ghetto в сообщении #847299 писал(а):

2. Имеет ли смысл $I_{rs} + I_{sr}$? Как можно слагать матрицы с разным кол-вом рядов и коллон?

почему с разным, и то и другое - квадратные матрицы порядка $m$ в Вашем случае

$I_{rs}$ есть матрица размером $m \times m$. У $A$ размер $m \times n$. Если обе они квадратные зачем обозначать их по-разному? Почему $I_{rs}$ к примеру не $m \times n$ матрица?

Тут $m =n$?


Что значит индекс матрицы $I_{rs}$? Я думал $r$ - это ряд, а $s$- это коллона. Также какая разница м/у $I_{rs}$ и $I_{sr}$?

Спасибо.

[ИСН]

Какая-то тревожная последовательность вопросов. Например, пришёл человек, спрашивает про разведение тигров. Деловито записал все подробности - про сырое мясо и т.д. Под конец случайно выясняется, что он считает тигров разновидностью бабочек.
Также у меня рождаются сомнения, правильно ли я понял, что такое $I_{rs}$. А что это такое, really? Написано красиво, спору нет, но... не лучше ли сказать словами?

[ghetto]

ИСН в сообщении #847355 писал(а):

Какая-то тревожная последовательность вопросов. Например, пришёл человек, спрашивает про разведение тигров. Деловито записал все подробности - про сырое мясо и т.д. Под конец случайно выясняется, что он считает тигров разновидностью бабочек.
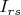
Также у меня рождаются сомнения, правильно ли я понял, что такое $I_{rs}$. А что это такое, really? Написано красиво, спору нет, но... не лучше ли сказать словами?

Слова автора учебника(мне с этого трудно сделать какие либо выводы):

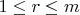
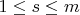
Let $1 \le r \le m$ and $1 \le s \le m$. Let $I_{rs}$
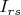
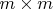
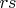
be the square $m \times m$ matrix which has component $1$ in the $rs$ place, and
$0$ elsewhere.

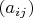
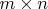
Let A = $(a_{ij})$ be any $m \times n$ matrix. What is the effect of multiplying
$I_{rs}A$?

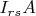
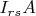
The definition of multiplication of matrices shows that $I_{rs}A$ is the matrix
obtained by putting the $s$-th row of $A$ in the $r$-th row, and zeros elsewhere.
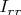
If $r = s$ then $I_{rr}$ has a component $1$ on the diagonal place, and $0$
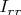
elsewhere. Multiplication by $I_{rr}$ then leaves the $r$-th row fixed, and replaces
all the other rows by zeros.

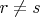
If $r \neq s$ let

$J_{rs} = I_{rs} + I_{sr}$

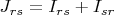
Then

$J_{rs}A = I_{rs}A + I_{sr}A$

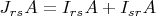
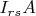
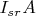
Then $I_{rs}A$ puts the $s$-th row of $A$ in the $r$-th place, and $I_{sr}A$ puts the
$r$-th row of $A$ in the $s$-th place. All other rows are replaced by zero.
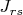
Thus $J_{rs}$ interchanges the $r$-th row and the $s$-th row, and replaces all
other rows by zero.

$Example$. Let

$$ J= \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix} $$

$$ A= \begin{pmatrix} 3 & 2 & -1 \\ 1 & 4 & 2 \\ -2 & 5 & 1 \\ \end{pmatrix} $$

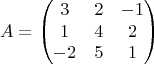
If you perform the matrix multiplication, you will see directly that $JA$
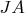
interchanges the first and second row of $A$, and replaces the third row by zero.


.

[gris]

Что Вас пугает? Матрица $A$ может быть и прямоугольной. Пусть $m=2;n=3$

$$ I_{21}= \begin{pmatrix} 0 & 0 \\ 1 & 0 \\ \end{pmatrix} $$

$$ I_{12}= \begin{pmatrix} 0& 1 \\ 0 & 0 \\ \end{pmatrix} $$

$$ A= \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} $$

$$I_{12}A= \begin{pmatrix} 4 & 5 & 6 \\ 0 & 0 & 0 \\ \end{pmatrix} $$

$$I_{21}A= \begin{pmatrix} 0 & 0 &0 \\ 1 & 2 & 3 \\ \end{pmatrix} $$

$$ J_{12}= \begin{pmatrix} 0& 1 \\ 1 & 0 \\ \end{pmatrix}$$

[ghetto]

gris в сообщении #847373 писал(а):

Что Вас пугает?

Из цытаты, которую я привел мне не понятно что такое $I_{rs}$. Например, как понимать индексы матрицы $J_{21}$?

edit: А, кажется понимаю. $I_{rs}$ -это матрица у которой все компоненты нули, кроме той, что описано в индексе. Значит индекс описывает местопoложение не-нулевой компоненты.

[gris]

Вы правильно предположили, что $I_{rs}$ это квадратная матрица размером $m\times m$, у которой элемент в строке с номером $r$ и столбце с номером $s$ стоит $1$, а в остальных местах нули. А$J_{rs}$ это квадратная матрица размером $m\times m$, у которой два элемента в строке с номером $r$ и столбце с номером $s$ и в строке с номером $s$ и столбце с номером $r$стоят $1$, а в остальных местах нули.

[ghetto]

gris в сообщении #847381 писал(а):

Вы правильно предположили, что $I_{rs}$ это квадратная матрица размером $m\times m$, у которой элемент в строке с номером $r$ и столбце с номером $s$ стоит $1$, а в остальных местах нули. А$J_{rs}$ это квадратная матрица размером $m\times m$, у которой два элемента в строке с номером $r$ и столбце с номером $s$ и в строке с номером $s$ и столбце с номером $r$стоят $1$, а в остальных местах нули.

Весь этот сыр-бор из-за невнимательного чтения.

Спасибо.

[ghetto]

quote

Пусть $E$ матрица, полученная из единичной $n \times n$ матрицы путем умножения ряда $r$ с числом $c$ и сложения его с рядом $s$, $r \neq s$. Пусть $A$ - $n \times n$ матрица . Тогда если помножить ряд $r$ матрицы $A$ на число $c$ и добавить его на ряд $s$ той же матрицы мы получаем $EA$.

$$ E = \begin{pmatrix} 1 & 0 & 4 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$

unquote.

У меня передоз от такого кол-ва переменных.

Пускай

$$ I_{rs} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} $$

Здесь ясно что значат $r$ и $s$ - индекс $s$ указывает на то, где нах-ся колонна на которой сидит элемент матрицы.Но если прочесть теорему выше, оба индекса $A$ вроде бы описывают ряд.

Пожалуйста, помогите разобраться с этими индексами.

[ИСН]

Сила математики в том, что она умеет использовать одни и те же буквы для разных целей. Я как-то описывал, кажется, что произошло с одним студентом, у которого кончились буквы.
Да, там это означает ряд строку и столбец. А здесь это означает строку и строку.
Жизнь - боль.

[ghetto]

ИСН в сообщении #847543 писал(а):

Сила математики в том, что она умеет использовать одни и те же буквы для разных целей. Я как-то описывал, кажется, что произошло с одним студентом, у которого кончились буквы.
Да, там это означает ряд строку и столбец. А здесь это означает строку и строку.
Жизнь - боль.

По определению выше, строки $A$ считаются $i = 1, \ldots, s, \ldots m$ если $I_{rs}$. Если поменять местами индексы $I_{rs}$ на $I_{sr}$, то тогда логично, что у $A$ строки пойдут $i = 1, \ldots, r, \ldots m$. $I_{sr}$ нам нужен потому, что $E = I + cI_{sr}$ и $AE = A + cI_{sr}A$.


Тогда ясно зачем автору понадобилось использовать $r$ и $s$ в качестве указателя строк $A$.

Только все это доходит до меня на седьмой день после прочтения.