Пусть имеется модель:

где

. Тут

- наблюдаемые переменные, а

- скрытая.

- шум, который не зависит от

.
Пусть

и

. По выборке

необходимо оценить параметры распределения
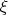
и

.
Используем следующую оценку: пусть

и

, где

. Тогда параметры распределения оцениваются как с.а. и с.к.о., а

является решением системы уравнений:

Нужно составить программу на языке R, которая будет оценивать данные параметры. В моём коде используются следующие обозначения:

(Оффтоп)
Код:
#POLYNOMIAL MODEL WITH NORMAL DISTRIBUTION
#g=g(x)=(x^d1, x^d2, ..., x^dn), where x:=xi and (d1, d2, ..., dn):=degrees
g <- function(xi, degrees) {
t(t(replicate(length(degrees), xi)) ^ degrees)
}
#generate.sample of size size with xi~N(alpha[1], alpha[2]) and epsilon~N(0, noise[1]), delta~N(0, noise[2])
#zeta have form beta^T * g(xi)
generate.sample <- function(size, alpha, beta, noise, degrees, g) {
xi <- rnorm(size, alpha[1], sqrt(alpha[2]))
x <- xi + rnorm(size, 0, sqrt(noise[2]))
y <- g(xi, degrees) %*% beta + rnorm(size, 0, sqrt(noise[1]))
data.frame(x, y)
}
#est.alpha estimation of normal distr. parameters: mu, sigma^2
est.alpha <- function(x, sigma.delta) {
c(mean(x), sd(x) ^ 2 - sigma.delta)
}
#psi is a conditional distribution xi|x~N(mu.psi, sigma.psi^2)
get.psi <- function(x, alpha, sigma.delta) {
matrix(c(alpha[1] * sigma.delta + x * alpha[2], replicate(length(x), alpha[2] * sigma.delta)) / (alpha[2] + sigma.delta), ncol=2)
}
#get.moment calculates moment's moment of normal random variable with mean mu and variance var
#this function calculates all moments up to 4th.
get.moments <- function(mu, var) {
matrix(c(replicate(length(mu), 1),
mu,
mu ^ 2 + var,
mu ^ 3 + 3 * mu * var,
mu ^ 4 + 6 * (mu ^ 2) *var + 3 * var ^ 2),
ncol=5)
#higher moments have to be added
}
#m=E(y|x)
m <- function(beta, psi.moments) {
as.matrix(psi.moments) %*% beta
}
#v=D(y|x)
v <- function(beta, psi.moments, degrees, sigma.epsilon) {
result <- replicate(nrow(psi.moments), 0)
temp <- c(0, 0, 0, 0, 0)
temp[degrees + 1] <- beta
beta <- temp
for(i in degrees)
for(j in degrees)
result = result + (psi.moments[, i + j + 1] - psi.moments[, i + 1] * psi.moments[, j + 1]) * beta[i + 1] * beta[j + 1]
result + sigma.epsilon
}
#dm=grad_beta m
dm <- function(psi.moments) {
psi.moments
}
LS <- function(x, y, beta, noise, degrees) {
alpha <- est.alpha(x, noise[2])
psi <- get.psi(x, alpha, noise[2])
psi.moments <- get.moments(psi[, 1], psi[, 2])
t(dm(psi.moments[, degrees + 1])) %*% ((y - m(beta, psi.moments[, degrees + 1])) / v(beta, psi.moments, degrees, noise[1]))
}
Я написал все функции, кроме "решателя". Хочу спросить совета по программе, поскольку некоторые моменты (например, функция v) мне не нравятся.
(Оффтоп)
P.S.: моя первая программа на R




