Кажется, решил.
Я рассмотрел всю игру по ходам. Пусть событие

- выигрыш первого игрока,

- выигрыш на 1 ходе, на 3 ходе, на 5 ходе (нумерация с учетом ходов другого игрока).
1 ход.

3 ход.


- 1 игрок вытащил черный шар на 1 ходе.

- 2 игрок вытащил черный шар на 2 ходе.


5 ход.



- 1 игрок вытащил черный шар на 3 ходе.
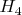
- 2 игрок вытащил черный шар на 4 ходе.

И
 -- 06.03.2014, 17:42 --
-- 06.03.2014, 17:42 --Посмотрел в ответ, и это решение опять неверное.
-- 06.03.2014, 17:49 --Ура, это всего лишь ошибка по невнимательности.

. И всё сходится.