В

определена функция

двух переменных

и

.
При каких
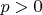
она является метрикой, а при каких - нет?
То, что она не является метрикой при

я доказывал так:
Первые две аксиомы доказаны для всех p. Достаточно указать три точки, такие, что для любых p

неравенство треугольника не имеет места.
Я взял точки

и

.
Если теперь я докажу, что существует число

, такое, что

, то я докажу, что при

представленная функция не является метрикой.
Будем искать такое

:




,
но имеет место

,
тогда можно принять

, а

.
Верно ли это доказательство?
И как доказать тот факт, что при

функция - метрика?