В сети есть такое решение этой задачи.
http://algolist.manual.ru/maths/geom/datastruct.php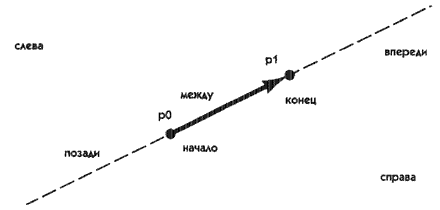
Код:
class Point {
public:
double x;
double у;
Point(double _x = 0.0, double _y =0.0);
// Опустим ненужные элементы класса
.......
enum {LEFT, RIGHT, BEYOND, BEHIND, BETWEEN, ORIGIN, DESTINATION};
// СЛЕВА, СПРАВА, ВПЕРЕДИ, ПОЗАДИ, МЕЖДУ, НАЧАЛО, КОНЕЦ
int Point::classify(Point &p0, Point &pl)
{
Point p2 = *this;
Point a = p1 - pO; // 1
Point b = p2 - pO; // 2
double sa = a. x * b.y - b.x * a.y; // 3
if (sa > 0.0)
return LEFT;
if (sa < 0.0)
return RIGHT;
if ((a.x * b.x < 0.0) || (a.y * b.y < 0.0))
return BEHIND;
if (a.length() < b.length())
return BEYOND;
if (pO == p2)
return ORIGIN;
if (p1 == p2)
return DESTINATION;
return BETWEEN;
}
Point Point::operator- (Point &p)
{
return Point (x - р.х, у - p. у);
}
Я знаю, что чтобы определить положение точки слева или справа относительно прямой, достаточно подставить координаты этой точки в уравнение прямой и посмотреть на результат. Если он отрицателен, то точка лежит слева, если положителен, то точка лежит справа. Если же результат равен нулю, то точка принадлежит прямой. Как я понимаю, в это куске кода делается нечто похожее.
1)
Код:
Point a = p1 - pO;
Point b = p2 - pO;
Векторы

и

начинаются в начале координат и заканчиваются в точках

и

. В результате вычитания мы получаем новый вектор

. Аналогично с вектором

. Я правильно понял смысл этих двух строк?

Начало и конец векторов рисовал специально, чтобы не накладывались друг на друга, иначе не видно направления вектора.
2)
Код:
double sa = a. x * b.y - b.x * a.y;
Я не пойму, что делает этот код. Напоминает уравнение прямой в виде

пожалуйста, помогите разобраться.