
Here we are.

Let
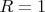
, axis
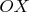
be bisector of the
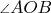
,
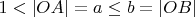
,

. For a point

we will designate its coordinates as
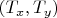
. Then
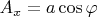
,
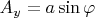
,
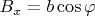
,
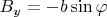
. We will make an exception for

, having its coordinates to be
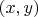
for brevity.
For line with equation
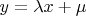
the square of the distance from
to it is
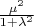
. For

to be bisector of the
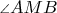
we need distances from
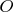
to
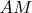
and to
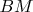
to be equal and to have

and

to be on different sides of

. The last condition boils down to

belongs to arcs

and
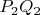
.
Having coordinates of points

,

, and

, the calculation of distance is easy. The condition of equedistance becomes


















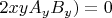
. The first factor is equation of line
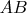
and is of no interest for us. The second factor is more interesting. Using polar form of coordinates for

and

we get much more manageable expression:



. Now we note that

belongs to unit circle and therefore
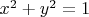
. So finally


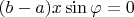
. Or,
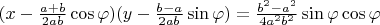
— an equation of a hyperbola.
Of course we need to consider case
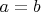
when the hyperbola reduces to pair of lines

and
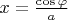
. The horizontal line intersects arcs in points
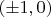
, the vertical does not intersect arcs. So in this case we have exactly two points in the locus.
In following we will assume
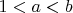
— all inequalities are strict.
Some properties of this hyperbola:
1) Its axises are parallel to the coordinate axises.
2) The intersection (point

) of axises is always inside rectangle
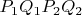
. As we assumed
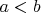
, both
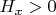
and
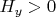
.
3) Point
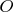
always belongs to the hyperbola.
4) Immediate consequence is that the hyperbola intersects the arc
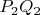
in exactly one point.
5) Each intersection of the hyperbola and circle has unique

coordinates (the function is monotonic in each segment

and
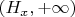
).
Therefore, to find number of points in the locus we need to find how many intersections we have with the arc

, id est how many solutions of the system:

First, we will solve second equation for

:
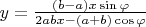
. Next, we will substitute

in the first equation with this expression and simplify result:




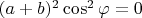
. Thirdly, we will replace

with
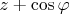
, thus making the last inequality equivalent to

:




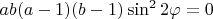
.
We are ready to apply the Descartes' rule of signs to this equation. The number of positive roots is equal to number of sign changes in the list of coefficients, or less than that by even number. Marking positive coefficients with + and negative with -, we have ++??-. The only way we can have more than 1 root is if ?? = -+, that is
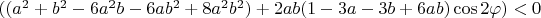
and
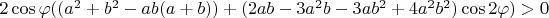
. Because coefficients for
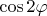
are positive, we have that
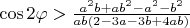
and
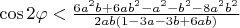
simultaneously. Therefore
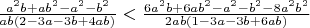
which is never true for
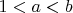
.
All together now! We have exactly one intersection on the arc
and exactly one intersection on the arc

.



