kekocaumay писал(а):
я еще не понимаю твое решение, можно объяснять ясно !
Вы про первую задачу?
AD писал(а):
Задание "описать структуру", конечно, весьма расплывчато.
Что значит "описать структуру? Понять, как оно выглядит?
Ну вот рисуете
достаточно крупно отрезок
![$A_0=[0,1]$ $A_0=[0,1]$](https://dxdy-01.korotkov.co.uk/f/4/2/2/4226617c40e2fc927f61dd67e9e9f5b582.png)
... нарисовали?
Заштрихуйте те числа, у которых в первом разряде нолик. Что это будет? Это будет просто
![$B_1=[0,1/2]$ $B_1=[0,1/2]$](https://dxdy-04.korotkov.co.uk/f/b/a/9/ba97761af7e8a81a9cad261a0d8fbf1f82.png)
. Эти числа в наше множество не входят, их надо выкинуть, получится множество

.
Заштрихуйте те числа, у которых в третьем разряде нолик. Что это будет? Это будет просто
![$$B_2=[0,1/8]\cup[1/4,3/8]\cup[1/2,5/8]\cup[3/4,7/8]$$ $$B_2=[0,1/8]\cup[1/4,3/8]\cup[1/2,5/8]\cup[3/4,7/8]$$](https://dxdy-02.korotkov.co.uk/f/9/6/a/96a9404b58995b002d691c83d9ac8c1182.png)
Эти числа в наше множество не входят, их надо выкинуть, получится множество

.
и т. д., попробуйте провести еще несколько итераций.
Наше множество есть

, потому что

- это множество чисел, у которых в разрядах

стоят единички, а

- это множество чисел у которых
во всех нечетных разрядах стоят единички, уловили?
Мера множества

есть
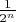
, поэтому мера множества

должна быть меньше
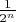
для всех

, откуда

.
Со второй задачей понятно?