Нахождение проекции момента импульса

[DewDrop]

Волновая функция некоторой системы в сферических координатах определяется выражением (А-нормировочная константа):
$\Psi = AR(r)sin^2 \theta sin 2 \varphi$. Причем,

$$\int_{0}^{\infty} R^2(r)r^2 dr = 1$$

Какие значения квадрата и z-проекции момента импульса могут быть измерены в этом состоянии? Каковы вероятности их измерения и средние значения?
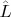
Я понял так: надо разложить по сферическим функциям, являющимся собственными состояниями операторов, $\hat{L}$ и $\hat{L_z}$.
Получится , что-то вида: $R(r) \fraq{\sqrt{15}}/ {2i}(Y_{22}+Y_{2-2}) $ (1) , где Y - сферические функции.
Смущает, что вероятность при таком коэффициенте больше 1 (модуль в квадрате).
А нашел из условия нормировки исходной функции: $\Psi^* \Psi dV = 1$
Пользуясь формулой sin через экспоненты получил выражение (1), учитывая что $Y_{2\pm2} = \sqrt{3/48}\sin^2(\theta) \exp^{\pm 2i \varphi}$. Затем перемножил А с тем что "не свернулось"(вышло из сферических функций).
И как понять, что соответствует значению и вероятности квадрата импульса, а что проекции z?
И как пользуясь этим найти средние значения или тут надо по определению, не опираясь на полученные данные?

[warlock66613]

DewDrop в сообщении #802801 писал(а):

читывая что $Y_{2\pm2} = \sqrt{3/48}\sin^2(\theta) \exp^{\pm 2i \varphi}$

По-моему это как раз ненормированные сферические функции. У нормированных под корнем $45 \over 96\pi$. Может у вас поэтому норма не сходится?

[DewDrop]

Да, похоже на то, коэффициент получается равным $\sqrt{2}/2i$

[Munin]

DewDrop в сообщении #802801 писал(а):

И как понять, что соответствует значению и вероятности квадрата импульса, а что проекции z?

Надо смотреть на индексы сферических функций - они показывают $l$ и $m.$

Вероятности и средние значения считаете из получившегося разложения по сферическим функциям.

[DewDrop]

Munin, вероятности понятно как найти, а средние значения?

[Munin]

$\overline{A}=\langle\mathrm{state}|A|\mathrm{state}\rangle$

[DewDrop]

Эм... простите, а что это означает?)

[warlock66613]

Ещё можно тупо найти все значения, а дальше зная все значения и их вероятности посчтитать обычным образом среднее. Но способ Muninа красивее конечно, органичнее, а кроме того даёт повод рассказать о брэкетах, кои есть совсем не бесполезная в квантовой механике штука.

[Чтобы найти собственные значения надо подействовать соотвествующим оператором на собственную (то бишь в данном случае шаровую) функцию: $\hat{L}_z\psi=L_z\psi$. Тут $L_z$ без крышки - это и есть собственное значение, число, что получится в результате измерения. Аналогично для квадрата. $\hat{L}_z Y_{l m}$ и $\hat{L}^2 Y_{l m}$ самому можно не считать, а найти в справочнике (учебнике, лекциях).]

[Munin]

DewDrop в сообщении #802862 писал(а):

Эм... простите, а что это означает?)

Бра-кет обозначения ЛЛ-3 § 11.

[DewDrop]

$<\hat{L^2}>=\hbar^2$ ?

[warlock66613]

DewDrop в сообщении #802901 писал(а):

$<\hat{L^2}>=\hbar^2$ ?

Не угадали.

[DewDrop]

Я по теории плаваю, а решить надо)

-- 18.12.2013, 01:56 --

$\hbar^2 l(l+1) =6 \hbar^2 $

[warlock66613]

DewDrop в сообщении #802909 писал(а):

$\hbar^2 l(l+1) =6 \hbar^2 $

Угу.