Если бы вы внимательней читали, то увидели бы, что свет летит в пространстве с геометрией Евклида или Лобачевского, что то же самое (только второй случай значительно длиннее) , что и геометрия пространства описывается геометрией Евклида или Лобачевского.
Свет не позволяет измерять расстояния. А мерная верёвка - позволяет. Поэтому геометрия Евклида и геометрия Лобачевского описываются всё-таки не светом, а мерной верёвкой. Если вы описали распространение света - это "недозаданная" геометрия, например, для геометрии Евклида это будет геометрия Евклида с точностью до масштабных преобразований. Видимо, именно так вы и воображаете себе геометрию Лобачевского, но это ошибка.
Это спорный вопрос - можно посмотреть определение метра. Там как раз физики всего мира измеряют метр светом.
Вы написали, что интеграл единица и что могут найтись такие пределы интегрирования, что отрезок прямой (на плоскости Лобачевского) будет метр. А вот про метод выбора границ интегрирования (путём построения) не написали.
Метод выбора границ интегрирования - это увеличивать длину от нуля, пока она не станет единицей. Можно протянуть мерную верёвку вдоль прямой линии.
Если взаимно однозначно задать плоскость Лобачевского и участок Евклидовой плоскости, то можно сравнить отрезки на плоскости Лобачевского, которые соответствуют одинаковым "метрам" на плоскости Евклида.
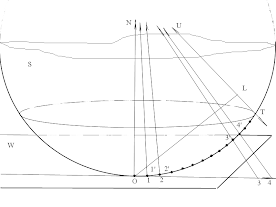
W - плоскость Лобачевского.
S - орисфера, которая касается W в точке О.
U прямая параллельная осям координат ON и O4.
Все остальные прямые 1, 2, 3, 4 - параллельны ON и пересекают 04
Ясно. что геометрия на орисфере - геометрия Евклида.
Ясно, что U на орисфере отсекает круг, радиусом равным радиусу кривизны.
Ясно. что остальные параллельные задают взаимно однозначно точки круга с геометрией Евклида и точки плоскости Лобачевского.
Отмерим на прямой, с точки зрения евклидовой геометрии, точки на расстоянии 1 метр. 0, 1', 2', 3' 4'.
Сопоставим эти отрезки с полученными на плоскости Лобачевского с помощью параллельных прямых 0, 1, 2, 3, 4.
Без особых доказательств видно, что на плоскости Лобачевского все отрезки, соответствующие метру разные.
-- 06.12.2013 01:31:13 --Давайте всё-таки вы назовёте учебники и другие источники по геометрии Лобачевского, на которые вы опираетесь. Это вопрос, ответ на который обязателен (даже если ответ - пустое множество).
Например, Ефимов "Высшая геометрия".