Путаете

просто базис, он задан как некоторые элементы

, образ на этих базисных векторах известен, раскладываем их по

, получаем матрицу в этом базисе.
Векторы

могут, конечно, составить базис, но к данной задаче этот факт отношения не имеет. Мы получили матрицу оператора, но не в базисе

. В каком? В исходном, старом. В том, в котором выражены и иксы, и игреки. Ниже только им я и буду пользоваться.
Что выражает матрица оператора? Её столбцы — это векторы, которые являются образами базисных векторов. Так,
образом вектора

является вектор

;
образом вектора

является вектор

;
образом вектора
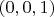
является вектор

.
Имея это, легко найти образ любого вектора. Например, проверим, что образом вектора

будет как раз

:

Но

был задан в исходном базисе, не в базисе

.
Раз мы можем найти в исходном базисе образ любого вектора, мы можем вообще забыть про набор из трех векторов

. Они ведь выделены из остального множества лишь тем, что для них были даны их образы.