Помогу правильно сформулировать задачу.
Дана СЛАУ

, где:

,

,

(неизвестное решение СЛАУ),
Причём известно, что

,

,

. Это свойство матрицы называется
диагональным преобладанием по строкам, обратите внимание:
не преобразованием, а
преобладанием.
Преобразуем исходную систему следующим образом: поделим каждое уравнение на соответствующий диагональный элемент: 1-е уравнение (т.е. строку

и компонент правой части

) поделим на
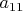
, 2-е уравнение --- на

, 3-е уравнение --- на

. В результате получится какая-то другая матрица (назовём её

), у которой единицы на главной диагонали (

), и какой-то другой вектор правой части (

). (на занятиях вы для удобства рассматривали расширенную матрицу 3x4, полученную простым приписыванием к матрице

вектора

справа, но это не меняет сути дела, просто мне привычнее рассматривать их отдельно).
Далее. На лекциях вы рассматривали метод простой итерации, который состоит в том, что выбирается какое-то начальное приближение

(это тоже
вектор, состоящий из компонентов

,

,

). И каждое следующее приближение строится по следующей формуле:

, где

,

--- единичная матрица. Поскольку у матрицы

также единицы на главной диагонали (как и у

), то их разность

будет иметь на главной диагонали нули.
Также на лекциях вы доказывали теорему, что при указанных условиях построенный итерационный процесс сходится к точному решению СЛАУ. Доказательство строится на лемме о сжимающем отображении, которая, в свою очередь, опирается на тот факт, что

(норма матрицы

) строго меньше 1.
Поэтому вопросы стоят так:
(1) Почему

меньше 1? (это должно было быть у вас в лекциях, на это опирается доказательство)
(2) Почему

будет меньше 1 и в том случае, когда у исходной матрицы

будет диагональное преобладание не по строкам, как было у вас на лекции, а по столбцам? Т.е. в том случае, когда

,

,

. Это именно то, что нужно доказать Вам.
Всё, что я до этого сделал --- это просто сформулировал задачу, используя правильные термины, не более. Учитесь правильно формулировать задачу, иначе Вас никто не поймёт!
Как доказать (2)? Во-первых, внимательно посмотреть на доказательство (1) у Вас в конспекте лекций и понять его, и во-вторых, попытаться действовать по аналогии.



