Радиус, кривизна и центр кривизны в точке (Зорич V.4.9)

[Urnwestek]

ewert в сообщении #786755 писал(а):

Не надо никаких омег. Введите произвольную зависимость угла от времени. После двукратного дифференцирования вектор ускорения совершенно явственно разобьётся на два слагаемых, одно из которых откровенно перпендикулярно радиус-вектору, а второе -- не менее откровенно параллельно. Чего и достаточно.

Я немного не понял, просто положить в моём решении $\omega(t) t = \alpha(t)$? Вроде как ничего поменяться не должно. То есть, грубо говоря, если в моём решении везде $\sin \omega t$ и $\cos \omega t$ заменить на $\sin \alpha$ и $\cos \alpha$, а $\dot{\omega}$ и $\ddot{\omega}$ заменить на $\dot{\alpha}$ и $\ddot{\alpha}$ то выйдет то, что просите меня сделать вы, если я правильно понял.

ewert в сообщении #786755 писал(а):

о почему-то напрочь забываете продифференцировать само время.

Этого ещё больше не понял. Ведь $\frac{d}{dt} t(t) = 1$, то есть если мы время дифференцируем по времени, то должна получится единица и это я, вроде, везде учитываю.

Что-то я слегка запутался.

[ewert]

Urnwestek в сообщении #786763 писал(а):

Ведь $\frac{d}{dt} t(t) = 1$,

Совершенно верно. И где она у Вас, эта единичка? Что такое производная произведения?...
Впрочем, это уже не актуально.

Urnwestek в сообщении #786763 писал(а):

просто положить в моём решении $\omega(t) t = \alpha(t)$? Вроде как ничего поменяться не должно.

Только не положить, а заменить бессмысленное левое на осмысленное правое.

Вы всё-таки выпишите на бумажке результат в новом варианте. А потом вглядитесь в него -- и просто сгруппируйте по производным первого и второго порядков.

[Urnwestek]

ewert в сообщении #786772 писал(а):

Вы всё-таки выпишите на бумажке результат в новом варианте. А потом вглядитесь в него -- и просто сгруппируйте по производным первого и второго порядков.

Да, штуки со вторыми производными оказались коллениарны вектору скорости, а с первыми — радиус вектору. Взял квадрат длины вектора скорости и поделил на длину вектора со штуками с первой производной и всё вышло. Спасибо.

ewert в сообщении #786772 писал(а):

Совершенно верно. И где она у Вас, эта единичка? Что такое производная произведения?...

$\frac{d}{dt} \omega(t) t =\dot{\omega}t + \omega$. Теперь понятно.

[ewert]

Urnwestek в сообщении #786783 писал(а):

Да, штуки со вторыми производными оказались коллениарны вектору скорости, а с первыми — радиус вектору.

Ну в смысле с точностью до наоборот. Да, верно.

[Urnwestek]

Отчего же наоборот?

$r(t) = (r\cos{\alpha},r\sin{\alpha})$
$v(t) = (-r\dot{\alpha}\sin{\alpha},r\dot{\alpha}\cos{\alpha})$
$a(t) = (-r\dot{\alpha}^2\cos{\alpha} - r\ddot{\alpha}\sin{\alpha},-r\dot{\alpha}^2\sin{\alpha} + r\ddot{\alpha}\cos{\alpha} )$

$(-r\dot{\alpha}^2\cos{\alpha},-r\dot{\alpha}^2\sin{\alpha}) (-\frac{1}{\dot{\alpha}^2}) = r(t)$
$(-r\ddot{\alpha}\sin{\alpha}, r\ddot{\alpha}\cos{\alpha}) \frac{\dot{\alpha}}{\ddot{\alpha}} = v(t)$

[ewert]

(Оффтоп)

Urnwestek в сообщении #786790 писал(а):

Отчего же наоборот?

От рассеянности. Я ведь тоже человек, не так ли?.. И тоже имею право удерживать в память готовый результат. И перепутать -- тоже имею.

Ну и перепутал; извините.

[Urnwestek]

ewert в сообщении #786795 писал(а):

От рассеянности. Я ведь тоже человек, не так ли?.. И тоже имею право удерживать в память готовый результат. И перепутать -- тоже имею.

Нет, что вы, я вас не упрекаю, спасибо вам за то, что вообще тратите на меня время, я просто всегда прежде всего допускаю вариант, что неправ — я, может я снова неправильно продифференцировал? (:

[ewert]

(Оффтоп)

Urnwestek в сообщении #786796 писал(а):

я просто всегда прежде всего допускаю вариант, что неправ — я

Это Вы очень правильно допускаете. Не ради самоуничижения, а просто ради эффективности это первое, что следует предположить; ну а потом уж -- пытаться то ли подтвердить, то ли опровергнуть своё мнение.

К сожалению, форумное общение вообще провоцирует безаппеляционность; и с этой провокацией в самом себе следует бороться. К счастью, здешняя модераторская политика мягко так, нежно, но этому препятствует.

[Urnwestek]

Хотелось бы доделать упражнение до конца:
c)
При движении по любой кривой, учитывая b), величину:
$r(t)=\frac{|v|^2}{|a_n|}$
естественно называть радиусом кривизны кривой в точке $(x(t),y(t))$
Покажите, что радиус кривизны вычисляется по формуле:
$r(t) = \frac{(\dot{x}^2 + \dot{y}^2)^{\frac{3}{2}}}{|\dot{x}\ddot{y} - \ddot{x}\dot{y}|}$

Ну тут подстановкой $|a_n| = |a| \frac{|(a,v_n)|}{|a||v|} \frac{|v|}{|v|}$ это просто показать.

d)
Величину, обратную радиусу кривизны, называют абсолютной кривизной плоской кривой в данной точке. Наряду с абсолютной кривизной рассматривается величина:
$k(t) = \frac{\dot{x}\ddot{y} - \ddot{x}\dot{y}}{(\dot{x}^2 + \dot{y}^2)^{\frac{3}{2}}}$
называемая кривизной.
Покажите, что знак кривизны характеризует направление поворота кривой по отношению к касательной. Выясните, какова размерность кривизны.

Размерность, как я пониманию $ \frac{\text{м}}{\text{c}^2} \cdot \frac{\text{с}^3}{\text{м}^3} = \frac{\text{с}}{\text{м}^2}$? Ведь в числителе стоит модуль ускорения, а в знаменателе куб скорости.

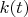
Что заметил: в числителе (а только от него зависит знак) $k(t)$ стоит векторное произведение ускорения на вектор скорости $[v,a]$ то есть. Знак векторного произведения положителен, если $a$ лежит по левую сторону от $v$ и отрицателен, если $a$ лежит по правую сторону от $v$. Вектор $v$ направлен вдоль касательной.

И тут я понял, что не понял задания. Что значит "характеризует направление поворота кривой по отношению к касательной"? В том смысле, что знак кривизны совпадает/противоположен со знаком $[v(t),r(t+h)-r(t)]$ при достаточно маленьких положительных $h$? То есть, геометрически, "росток" функции в точке $r(t)$ лежит по левую/правую сторону от касательной?

[ewert]

Urnwestek в сообщении #786822 писал(а):

Выясните, какова размерность кривизны.

Метры в минус первой. По определению кривизны. Тут Зорич просто в очередной раз наводит тень на плетень (он это любит).

[Urnwestek]

В знаменателе стоит квадрат скорости. Блин. Действительно метры в минус первой.

[Urnwestek]

Знак кривизны $k(t)$ зависит лишь от числителя (знаменатель положителен) а в числителе находится векторное произведение вектора скорости на вектор ускорения. Пусть $[v,a]>0$ это значит, что $[v,\lim\limits_{h\to 0} \frac{v(t+h)-v(t)}{h}]>0$, это означает, что существует такое $\delta$, что для любого $0<h<\delta$ будет выполнятся $[v,\frac{v(t+h)-v(t)}{h}]>0$, по свойствам определителя получим $\frac{1}{h}[v(t),v(t+h)]>0$ так как $\frac{1}{h}>0$ следовательно $[v(t),v(t+h)]>0$ это значит, что вектор $v(t+h)$ лежит по левую сторону от вектора $v(t)$. Что, собственно, и значит, что производная "поворачивает" против часовой стрелки.

Верно ли будет такое доказательство того, что знак кривизны характеризует направление поворота касательной?

[Urnwestek]

Нужна помощь с пунктом:
f)
Подберите константы $a,b,R$ так, чтобы окружность $(x-a)^2+(y-b)^2=R^2$ имела с данной параметрически заданной кривой $x=x(t)$, $y=y(t)$ в точке $x_0=x(t_0)$, $y_0=y(t_0)$ касание возможно более высокого порядка. Предполагается, что $x(t),y(t)$ дважды дифференцируемы и $(\dot{x}(t_0),\dot{y}(t_0))\neq(0,0)$.
Указанная окружность называется соприкасающейся окружностью кривой в точке $(x_0,y_0)$. Её центр называется центром кривизны кривой в точке $(x_0,y_0)$. Проверьте, что её радиус совпадает с определенным в b) радиусом кривизны кривой в точке.

Вроде понятно из геометрических соображений, что касательная к кривой в точке так же должна быть касательной искомой окружности, то есть, центр лежит где-то на прямой, перпендикулярной касательной и проходящей через $(x_0,y_0)$, но, во-первых, рисунок не доказательство, хотелось бы аналитического обоснования, а во-вторых, даже если и лежит он на этой прямой, как его дальше искать?

[forexx]

Используйте свойство: кривизна и радиус кривизны-величины взаимно обратные.

[Urnwestek]

forexx в сообщении #787199 писал(а):

Используйте свойство: кривизна и радиус кривизны-величины взаимно обратные.

Абсолютная кривизна и радиус кривизны, как я понимаю. (: Но тут-то, как я понял, требуют как раз то и доказать, что радиус кривизны — это радиус соприкасающейся окружности, а использовать то, что доказываешь — не комильфо. Или я неправильно понял ваше указание?