У меня была и другая идея. Что точка

лежит на плоскости, проходящей через
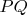
перпендикулярно ребру

. Это можно доказать, например, аналитически.
Будем рассуждать в общем виде. Пусть нам даны две точки

и прямая, скрещивающаяся с прямой
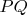
. Повернем систему координат так, что точки

лежат на оси

а прямая перпендикулярна плоскости

. Тогда можно считать, что их координаты

а прямая имеет уравнения

. Тогда искомая сумма расстояний равна

. Дифференцируя, получаем, что производная обращается в 0 только при

.
Может, это можно доказать строго геометрически.