









Получилось, что из того, что

следует то, что

Если всю логическую цепочку развернуть в обратную сторону, получится, что из того, что

будет следовать, что

.
А это и есть индукционный переход. База

Верно ли это?
-- 22.10.2013, 23:00 --Рассмотрим уравнение

корень этого уравнения

.
Поскольку последовательность не убывает

.
Тогда если
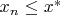
то

Поэтому последовательность ограничена сверху двойкой.
для доказательства того, что последовательность возрастает достаточно заметить, что при

возрастает функция

и что

Спасибо, понятно!