Проверка на равенство двух матриц

[VasRoG]

Здравствуйте, помогите пожалуйста вот с какой проблемой.

Есть две матрицы (X и Y) одинакового размера вещественных чисел. Каждое число - это угол, принимающий значения [0;2\pi].
Если элемент матрицы выходит за интервал [0;\pi], то его нужно вернуть в этот интервал т.е. вычесть\pi из имеющегося значения. (Условие 1)
Необходимо узнать равны ли эти матрицы.
На матрицу Y может воздействовать постоянная помеха z ([0;2\pi]) (ко всем элементам матрицы Y добавляется константа z), которая нам неизвестна.

Если не рассматривать условие 1, то я бы сделал так: вычислил среднее значение (мат. ожидание) двух матриц: ср_1 и ср_2. Причем, если матрицы равны (просто Y искажена помехой, а X - нет), то ср_2 = ср_1 + z. А дальше вычислил матрицы:
X_1 = X - ср_1
Y_1 = Y - ср_2
Т.о. избавился бы от неизвестной константной помехи z. Если X_1 и Y_1 равны, то и Y и X равны.
Теперь вопрос: а что делать, если нужно выполнение условия 1? Ведь т.к. помеха z может быть любой, то проверять условие 1 до вышеприведенной обработки нельзя (т.к. именно из-за помехи угол может стать большим \pi и вычтя \pi из имеющего значения мы придем к ошибке). А после обработки непонятно как проверить условие_1.
Столкните с места, а то уже 2 день клинит.

[Brukvalub]

Если исходные (необработанные и невозмущенные помехой) матрицы равны, то после действия помехи их разность будет матрицей, все элементы которой равны помехе.

[VasRoG]

Дело в том, что матриц много и они не сравниваются непосредственно. Нужно обработать их так, чтобы после обработки они были приведены к виду, из которого потом уже вычисляются характеристики, на основании которых и делается заключение о равенстве матриц.

[nworm]

Есть условие 1, нет условия 1, если можно поэлементно сравнивать две матрицы и эти две матрицы совсем не равны, то за 2-3 сравнения этот случай можно отсеять, выявив неравенство. То есть, если матрицы сильно друг от друга отличаются (не одна и та же немного искажённая матрица), то в среднем алгоритм будет работать довольно быстро.

Но поскольку матрицы непосредственно сранивать нельзя, то хотелось бы узнать, что делать можно.

[VasRoG]

Задача такая: есть база таких матриц, скажем N-штук. Мы знаем, что на всех них помеха не воздействовала. Есть алгоритм A, который нужно применить ко всем этим матрицам, чтобы из них вычленить какие-то характеристики. Например, алгоритм A - это вычисление определителя матрицы. (это только например) Таким образом применив алгоритм A ко всем матрицам мы получим базу данных из N-чисел.
Далее, нам поступает матрица Y (и мы знаем, что это одна из матриц, которая у нас уже обработана и ее характеристика(и)) находятся в базе данных), но эта матрица может быть искажена помехой вида:

Цитата:

На матрицу Y может воздействовать постоянная помеха z () (ко всем элементам матрицы Y добавляется константа z), которая нам неизвестна.

К матрице Y нам также следует применить алгоритм A и вычислить ее характеристику. Потом эта характеристика сравнивается со всеми характеристиками имеющимися в базе данных и определяется что же это за зверь - матрица Y.
Соответственно нужно создать алгоритм A.
С матрицами можно делать что угодно.
Но у меня вопрос как избавившись от помехи выполнить условие 1? (вычитая среднее согласно посту 1 мы, обрабатывая матрицы по отдельности, приходим к одинаковому их виду из которого уже потом можно вычислять какие-то характеристики) Может можно как-то по-другому избавиться от такой помехи?

[nworm]

Уважаемый VasRoG, следующий абац - исключительно моё личное мнение. А всё равно надо знать какие там матриы используются, одна картина когда одна матрица 7X7 и допускается изменение какого-то одного её элемента. И совсем другая картина, когда есть похожие матрицы 7x7 в которых различаются (по крайней мере незначительно) все 49 элементов. Надо таки либо математически задачу ставить , либо написать какие разделы радиотехники (или чего другого) стоит почитать чтобы понять какие используются матрицы (вообще, если кто не знает, практика показывает, что люди, которые помехами занимаются довольно хорошо в математике разбираются).

Напишу свой способ сравния двух матриц.
Гипотеза - две матрицы $A$ и $B$ равны. Пытаемся её опровергнуть.

Первое сравнение.
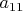
Сравниваем элементы $a_{11}$ и $b_{11}$.
Три варианта.
1. Оба элемента меньше $\pi$.
Находим разность $\Delta=b_{11}-a_{11}$
2. Только один элемент меньше $\pi$ (пусть это $b_{11}$).
Тогда либо $\Delta _1=b_{11}-a_{11}$, либо $\Delta _2=b_{11}-\pi-a_{11}$
3. Оба элемента больше или раны $\pi$.
Тогда либо $\Delta _1=b_{11}-a_{11}$, либо $\Delta _2=b_{11}-\pi-a_{11}$, либо $\Delta _3=b_{11}-\pi-a_{11}-\pi$, либо $\Delta _2=b_{11}-a_{11}-\pi$.

Второе сравнение аналогично первому, только здесь уже может произойти отсеивание неравенств матриц.
Считаем $\Delta$ и, если множество полученных дельт не пересекается с тем, что получено раньше - всё отсеиваем неравные матрицы, в другом случае - хорошо идём дальше, сужаем множество дельт.

Если матрицы неравные, алгоритм достаточно быстро останавливается, если же равные, то придётся проверить все элементы.

Но всё рассмотренное - для случая, когда есть похожие матрицы, в которых различаются (по крайней мере незначительно) все 49 элементов.

[nworm]

Если ничего не известно об исследуемых матрицах, то характеристика матриц, которую можно использовать для сравнения содержит в себе столько же информации сколько и сама матрица, т.е. требует для своего хранения столько же памяти.