How is pressure on an object ?

[m441]

No at all. But I don't understand, you said balls are unstable but in this case there is a problem because something in the center can recover energy, and after you said if there is another non-electrostatic object balls can be stable. So in my system, balls are stable or not ?

[Oleg Zubelevich]

Surely they are not

[m441]

ok, so if the number of balls is not infinite (I imagine a number like I drawn on figure), if I put something in the center that can turn around the center, it's possible to recover energy ? So, in this case what lost energy if ball is a magnet ball or electrostatic ball ?

[Sender]

All balls will fall on the outer circle and become stable.

[m441]

Ok, so I put balls like 1 and after all balls will go like 2 ? It's possible to have this type of combination of mouvement ?

And if I add 20 more balls, and after 20 balls, etc. it's the same all balls will go to the outer circle ?

like that:

[Munin]

Sender в сообщении #760331 писал(а):

In this case Gauss's flux theorem is applicable and it is easy to show that all balls will be located at the surface of the outer spheric shell.

I totally forgot about this. I am very sorry.

(Though, in this case, the pressure would be also equal, zero. But, for more general long-range forces, my reasoning becomes wrong. Such sets of particles do not behave as a media in the limit.)

-- 05.09.2013 00:32:18 --

m441 в сообщении #760354 писал(а):

I can't understand how the density can be the same !

That was just wrong in my original reasoning.

-- 05.09.2013 00:35:18 --

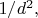
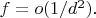
For the balls to behave more like some media, they should have a short-range law of interaction, that is, force is something smaller than $1/d^2,$ it can be written as $f=o(1/d^2).$ There are many such laws in physics: intermolecular interaction, internucleon interaction, weak interaction, anything Yukawa-like between quasiparticles in the condensed matter physics.

[m441]

so, in my last message, if I put 20 balls, ok they go to the outer circle, but if I add 20 more, and more, etc. All particules will be at outer circle ? but if particles has radius, it's not possible to put infinite number. So, a second layer would appear, etc. And it's possible to "full" circle. If I try to estimate sum of force, I need to take all forces from all balls. At outer circle the pressure must be higher than at center (it's that I think). If not, can you explain ?

[Munin]

m441 в сообщении #760580 писал(а):

so, in my last message, if I put 20 balls, ok they go to the outer circle, but if I add 20 more, and more, etc.

They all would go to the outer surface all the same.

m441 в сообщении #760580 писал(а):

but if particles has radius, it's not possible to put infinite number. So, a second layer would appear, etc. And it's possible to "full" circle.

"full" -> fill

Yes, it is possible. By the way, the law for the balls of nonzero radius should be written as

$$\left\{\begin{array}{ll}f\propto 1/d^2&\qquad\text{if }d>d_0\\V=+\infty&\qquad\text{if }d\leq d_0\end{array}\right.$$

But the internal balls would "lie" on the outer layers, and put no pressure on any internal objects.

[m441]

ok, if I understood, at outer circle there are particules with exactly the same pressure and at internal no particle so with no pressure, is that ?

[Munin]

Yes.

[Sender]

If you have enough balls to form several layers on the outer surface, the pressure will increase from inner layers to outer and reaches its maximum at the outer bound.
In specific case of Coulomb interaction ($F=\gamma\frac{q_1q_2}{r^2}$) we can try to obtain exact expression for it.
At the marginal case when size of a ball tends to zero we can introduce volumetric charge density $\rho$, balls form a layer of charged material.
Let $R$ be a radius of the outer spheric shell and $h$ - net thickness of charged layer. Let $p(x)$ be a pressure at radius $x$. Obviously, $p(x)=0$ if $0 \leqslant x <R-h$.
Now let us consider the case when $R-h \leqslant x \leqslant R$.
Inside of radius $x$ we have charge $q(x)=4\pi \rho\int_{R-h}^{x}t^2 dt=\frac{4\pi \rho}{3}(x^3-{(R-h)}^3)$.
So, spherical layer of thickness $dt$ at radius $t$ contributes to the pressure in outer layers

$$dp=\rho \gamma \frac{q(t)}{t^2}dt=\frac{4}{3} \pi \rho^2 \gamma \frac {t^3-{(R-h)}^3}{t^2}dt$$

Let

$$\frac{4}{3} \pi \rho^2 \gamma=k$$

Finally,

$$p(x)=\int_{R-h}^x k \frac {t^3-(R-h)^3}{t^2}dt=k (\frac{t^2}{2}+\frac{{(R-h)}^3}{t})\vert_{R-h}^x=k (\frac{x^2-{(R-h)}^2}{2}+{(R-h)}^3(\frac{1}{x}-\frac{1}{R-h}))=$$ $$=k(\frac{x^2}{2}+\frac{{(R-h)}^3}{x}-\frac{3}{2}{(R-h)}^2).$$

[m441]

Ok, many thanks ! Merci beaucoup !! so the pressure change in thickness where there are particules and it's 0 in the center. Now, with an object in the center, a part of object is without particules around and a part is in the tickness where there are particules, it's the same ? Object change the pressure or not ? I think it must in the contrary, the sum of forces is not 0.

[Munin]

(Offtopic)

To make formulas more pretty, you can use \left( ... \right) for high parens, and \Big| for high vertical bar.

-- 05.09.2013 10:39:28 --

m441 в сообщении #760634 писал(а):

so the pressure change in thickness where there are particules and it's 0 in the center. Now, with an object in the center, a part of object is without particules around and a part is in the tickness where there are particules, it's the same ?

Yes, it is the same. The parts of object, that sink into the layer of particles, would feel the pressure like the bottom of a boat, sunken into the water.

-- 05.09.2013 10:52:53 --

Munin в сообщении #760635 писал(а):

The parts of object, that sink into the layer of particles, would feel the pressure like the bottom of a boat, sunken into the water.

That's not right. For the water, parts of object substituting the water, would not change the gravitational force towards other water. For this problem, parts of object substituting the charged particles, would diminish the charge, and thus the function $p(x).$

[Sender]

Particularly, particles will tend to push the body out of their layer, so this is not a situation of equillibrium.

[m441]

Цитата:

For this problem, parts of object substituting the charged particles, would diminish the charge, and thus the function $p(x).$

and if the object is charged for compensate the lack of charged ?

Цитата:

so this is not a situation of equillibrium.

the object can be fixed like circle, support of the system must have sum of force to 0 I think.