IMO 2013

[sopor]

Задача 1.
Индукция по $k$. База $ k=1$ - очевидно, берем саму дробь.
Пусть теперь даны произвольные $ k>1$ и $n$. Заметим, что у дроби $1+\frac {2^k-1}{n}=\frac {n+2^k-1}{n}$ числитель и знаменатель разной четности. Если числитель четен, то домножаем нашу дробь на $\frac {n}{n+1}$, если же нет, то на $\frac {n+2^k-2}{n+2^k-1}$. В обоих случаях после сокращения одинакового множителя у нас получится дробь, у которой и числитель и знаменатель четны, и разность между ними равна $2^k-2$. Сократим на $2$, тогда разность станет равна $2^{k-1}-1$, и для этой дроби используем индукционное предположение. Пример: исходная дробь $1+\frac {15}{11}=\frac {26}{11}$. Домножаем на $\frac{11}{12}$, получаем $\frac {26}{12}$, сокращаем на $2$ и имеем дробь $\frac {13}{6}=1+7/6$. К ней применяем инд. предположение.

[dm]

Мои фото: https://www.facebook.com/media/set/?set ... 039&type=3
http://vk.com/album5499034_177592450

[dm]

Открытие
http://youtu.be/WWKMT7HuRgM
http://youtu.be/5o4_eqVYTGY
http://youtu.be/AQR1cfnpzmI
http://youtu.be/oCnTumYIfZ4
http://youtu.be/0R52hoqE1Hs
http://youtu.be/fErsiEhR1mU

[dm]

Закрытие
http://youtu.be/QN9n33SzQ80

[dm]

Итоговое заседание жюри
http://youtu.be/BMpD4p5X7t8

[Dave]

Задача 6.

На всякий случай, вначале официальный перевод условия.
Пусть $n \geqslant 3$ — целое число. Рассмотрим окружность и $n+1$ точек на ней, разбивающих её на равные дуги. Рассмотрим все способы пометить эти точки числами $0,1,\dots,n$ так, что каждое число использовано ровно один раз. Два способа, отличающихся поворотом, считаются одинаковыми. Способ пометки называется красивым, если для любых четырех меток $a<b<c<d$ таких, что $a+d=b+c$, хорда, соединяющая точки с метками $a$ и $d$, не пересекает хорду, соединяющую точки с метками $b$ и $c$.
Пусть $M$ — количество красивых способов пометки. Пусть $N$ — количество упорядоченных пар $(x,y)$ натуральных чисел, удовлетворяющих условиям $x+y \leqslant n$ и $\text{НОД}\,(x,y)=1$. Докажите, что

$$M=N+1.$$

Решение.
Ясно, что важен только взаимный порядок расположения чисел на окружности, но никак не их конкретные координаты, поэтому уберём условие равенства дуг, а "поворот" заменим перечислением порядка от нуля. Возьмём любой способ пометки и сопоставим ему перестановку

$$\begin{pmatrix} 0 & 1 & \dots & n \\ x_0 & x_1 & \dots & x_n \end{pmatrix},$$

где под каждым числом написано следующее за ним на окружности по часовой стрелке число. Ясно, что разным способам пометки соответствуют разные перестановки и каждая перестановка порождает не более одного способа пометки. Далее будем отождествлять способ пометки с описывающей его перестановкой и будем называть перестановку красивой, если она задаёт красивый способ пометки.
Пусть $1 \leqslant p \leqslant n$, $1 \leqslant q \leqslant n$, $p+q>n$. Определим перестановку

$$G(p,q,n)=\left(\begin{array}{cccc|ccc|cccc} 0 & 1 & \dots & n-p & n-p+1 & \dots & q-1 & q & q+1 & \dots & n \\ p & p+1 & \dots & n & n-q+1 & \dots & p-1 & 0 & 1 & \dots & n-q \end{array}\right)$$

(средняя группа может отсутствовать при $p+q=n+1$).

Лемма. Перестановки вида $G(p,q,n)$, где $1 \leqslant p \leqslant n$, $1 \leqslant q \leqslant n$, $p+q>n$, а также $\text{НОД}\,(p,q)=1$, и только они, являются красивыми.

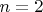
Доказательство проведём индукцией по $n$. В качестве базы индукции выберем $n=2$. $G(1,2,2)$ и $G(2,1,2)$ определяют все возможные расположения чисел $0,1,2$ на окружности (соответственно по часовой и против часовой стрелки), которые, ввиду отсутствия указанных в условии задачи четвёрок, условно могут считаться красивыми способами пометки.
Найдём все красивые перестановки для заданного $n \geqslant 3$, если уже доказано, что все красивые перестановки для меньших $n$ имеют вид, указанный в условии леммы (в частности, это означает, что каждая такая перестановка задаёт какой-либо способ пометки, т.е. порождает ровно один цикл, а не разбивает группу чисел от $0$ до $n$ на меньшие циклы). Ясно, что каждый красивый способ размещения чисел $0,1,\dots,n$ заключается во вставке числа $n$ в красивый способ размещения $0,1,\dots,n-1$, т.к. условие непересечения хорд должно быть верно, в частности, при $d \leqslant n-1$. При этом необходимо и достаточно, чтобы это условие непересечения выполнялось дополнительно при $d=n$ и любой соответствующей тройке остальных чисел $a$, $b$, $c$. Возьмём любую перестановку $G(p,q,n-1)$, $1 \leqslant p \leqslant n-1$, $1 \leqslant q \leqslant n-1$, $p+q>n-1$, $\text{НОД}\,(p,q)=1$. Рассмотрим два случая.
1) $p+q>n$. В этом случае вторая группа столбцов в $G(p,q,n-1)$ непуста. Рассматривая первые столбцы в каждой группе, видим, что числа $q,0,p$ должны идти подряд по часовой стрелке именно в таком порядке, а число $n-q$ идёт сразу за $n-p$. Но это означает, ввиду $0+n=p+(n-p)=q+(n-q)$, что $n$ мы можем вставить только между $n-p$ и $n-q$ и получить не что иное, как перестановку $G(p,q,n)$. В то же время эта перестановка всегда будет красивой. Действительно, каждая хорда, соединяющая $b$ и $c$ при $b+c=n$ должна, ввиду красивости $G(p,q,n-1)$, находиться целиком по одну сторону от обеих хорд $(p,n-p)$ и $(q,n-q)$, а значит не может пересекать лежащую между ними хорду $(0,n)$ в $G(p,q,n)$. Что же касается случая, когда $a>0$, то заметим, что если из $G(p,q,n)$ выбросить $0$, и вычесть $1$ из всех чисел, то получится опять $G(p,q,n-1)$. При этом, т.к. каждая четвёрка $(a,b,c,d)$ с $0<a<b<c<d=n$ и $a+d=b+c$ перейдёт в четвёрку $(a-1,b-1,c-1,d-1)$, а $G(p,q,n-1)$ - красивая перестановка, то хорды $(a-1,d-1)$ и $(b-1,c-1)$ в $G(p,q,n-1)$, а, стало быть, и $(a,d)$ с $(b,c)$ в $G(p,q,n)$, не будут пересекаться.
2) $p+q=n$. В этом случае $G(p,q,n-1)$ примет вид

$$\left(\begin{array}{cccc|cccc} 0 & 1 & \dots & q-1 & q & q+1 & \dots & n-1 \\ p & p+1 & \dots & n-1 & 0 & 1 & \dots & p-1 \end{array}\right).$$

Заметим, что, опять же, числа $q,0,p$ идут подряд, но на этот раз, ввиду равенства $0+n=p+q$, $n$ можно вставить только между $p$ и $q$, рядом с $0$. Здесь получаются два случая.
2a) При вставке $n$ между $q$ и $0$ получается перестановка $G(p,n,n)$.
2б) При вставке $n$ между $0$ и $p$ получается перестановка $G(n,q,n)$.
Обе новые перестановки всегда будут красивыми. Действительно, хорда $(0,n)$, ввиду своего крайнего расположения, пересекаться ни с чем не может, а случай $a>0$ сводится, как и в варианте 1, отбрасыванием $0$ и вычитанием $1$, к уже известной красивой перестановке, которой в обоих вариантах будет исходная $G(p,q,n-1)$.

(Оффтоп)

Можно даже доказать, что расположение чисел на окружности является красивым тогда и только тогда, когда оно самоподобно, т.е. отбрасывание $n$ или же отбрасывание $0$ и вычитание $1$ приводят к эквивалентным расположениям. Но это так, к слову.

Итак, мы получили следующие пути получения красивых перестановок (везде $1 \leqslant p < n$, $1 \leqslant q < n$, $\text{НОД}\,(p,q)=1$ ):
1) $G(p,q,n-1) \to G(p,q,n)$, $p+q>n$;
2а) $G(p,q,n-1) \to G(p,n,n)=G(p,p+q,n)$, $p+q=n$;
2б) $G(p,q,n-1) \to G(n,q,n)=G(p+q,q,n)$, $p+q=n$.
Видим, что во всех случаях новые тройки $(p',q',n)$ удовлетворяют условиям леммы. Обратно, если $p'$ и $q'$ таковы, что $1 \leqslant p' \leqslant n$, $1 \leqslant q' \leqslant n$, $p'+q'>n$, $\text{НОД}\,(p',q')=1$, то в случае, когда оба эти числа строго меньше $n$, полагаем $p=p'$, $q=q'$ (вариант 1), а в противном случае оставляем меньшее, а вместо другого, равного $n$, берём модуль их разности (вариант 2а или 2б) и получаем, следуя одному из перечисленных путей, что $G(p,q,n)$ порождает красивый способ пометки. Лемма доказана.

Теперь уже нетрудно доказать равенство $M=N+1$ в условии задачи. Заметим, что, при любом натуральном $p$, во всех отрезках целых чисел длины $p$ содержится одинаковое количество чисел, взаимно простых с $p$.

(Доказательство)

Кто-то сказал бы, что остаток от деления $q$ на $p$ целиком определяет взаимную простоту $p$ и $q$, я же предпочитаю использовать равенство $\text{НОД}\,(p,q)=\text{НОД}\,(p,q-p)$ и последовательно "перекидывая" один край отрезка на другой, получить из исходного отрезка конечный.

Поэтому $M$, будучи количеством элементов во множестве $\{(p,q) \mid 1 \leqslant p \leqslant n, \, 1 \leqslant q \leqslant n, \, p+q>n, \, \text{НОД}\,(p,q)=1 \}$, равном $\{(p,q) \mid 1 \leqslant p \leqslant n, \, n+1-p \leqslant q \leqslant n, \, \text{НОД}\,(p,q)=1\}$, также равно количеству элементов во множестве $\{(p,q) \mid 1 \leqslant p \leqslant n, \, 1 \leqslant q \leqslant p, \, \text{НОД}\,(p,q)=1\}$. Для завершения доказательства остаётся выбросить из последнего множества пару $(1,1)$, заметить, что тогда всегда $q<p$, и использовать соответствие $x=p-q, \, y=q$.

[Dave]

Своё решение 2-й задачи не привожу, потому что оно несколько длиннее хорошего решения товарища SCP с AOPS, любой желающий может посмотреть. А взамен предлагаю другую задачу, основанную на собственном решении.