Что такое связность?

[Nobody85]

Здравствуйте. Будьте добры, объясните наглядно, что такое линейная, и в частности, аффинная связность и как она связана с символами Кристоффеля. Заранее спасибо.)

[Munin]

Линейная и аффинная связность - это частные случаи общего понятия связности на расслоении. А связность Леви-Чивиты - частный случай аффинной связности.

Наглядно связность Леви-Чивиты можно представить себе так. Возьмём лист бумаги, и расчертим его параллельными линиями, проходящими через все точки. Потом ещё одной системой таких линий, но под другим углом. И так - подо всеми углами. Теперь, если мы выходим из какой-то точки по какой-то линии, то мы знаем, как эта линия идёт, когда мы пришли в другую точку. Назовём эти линии геодезическими. При помощи этих линий можно переносить вектор из точки в точку. 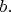Допустим, мы в точке 1 имеем вектор вдоль линии $a,$ и идём в другую точку вдоль линии $b.$ Тогда, придя в точку 2, мы должны будем взять вектор опять же в направлении линии $a',$ принадлежащей той же подсистеме линий, что и $a.$ Это другое представление о геодезических, чем через метрику. Метрика заставляет нас натягивать нитку вдоль поверхности, и кратчайшая линия называется геодезической. А связность Леви-Чивиты предлагает нам двигаться по поверхности, как на лыжах: мы не можем свернуть в сторону, потому что лыжи прямые, и не поворачиваются в лыжне (или можно представить себе рельсы). И таким образом, геодезической называется линия, которая "никуда не сворачивает". Разумеется, в проекции на плоскую карту геодезическая может выглядеть кривой - она "никуда не сворачивает" в смысле внутренней геометрии на поверхности.

Каким образом эта картина связана с общим понятием связности? Связность на расслоении - это когда мы в каждой точке пространства (оно становится базой) восстанавливаем некоторое новое пространство (слой), и задаём правила перехода между соседними слоями, так что двигаясь по определённому пути от точки к точке базы, мы получаем однозначное соответствие между слоями в начальной и конечной точке. Теперь, возьмём в качестве слоя касательную плоскость к искривлённой поверхности. Такое расслоение называется касательным расслоением. Взяв какие-то векторы на этой касательной плоскости, поедем по пути по поверхности - и наши векторы поедут вместе с нами. Это с одной стороны - правило переноса векторов по аффинной связности - а с другой стороны - эта процедура задаёт связность на касательном расслоении. Таким образом, аффинная связность - это и есть связность на касательном расслоении. А связность Леви-Чивиты - это аффинная связность без кручения. Кручение легко себе представить: это когда мы вместо линий, как в прошлый раз, расчерчиваем пространство тонкими полосками, и такие полоски могут быть закручены вокруг своей оси. Тогда мы имеем информацию не только о том, как проходят геодезические, но и как переносятся векторы - по другому правилу, чем "взять линию из подсистемы линии $a$".

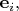
Символы Кристоффеля - это коэффициенты, выражающие связность в выбранном базисе. Они определены как $\Gamma^k_{ij}\mathbf{e}_k=\nabla_i\mathbf{e}_j,$ то есть, перенося вектор $\mathbf{e}_j$ в направлении вектора $\mathbf{e}_i,$ мы получаем компоненты в направлении векторов $\mathbf{e}_k,$ равные $\Gamma^k_{ij}.$

Линейная связность - это ещё более общее понятие, чем аффинная связность. Это ситуация, когда векторные пространства слоёв в каждой точке - не касательные, а просто какие-то векторные пространства. Даже любой другой размерности.

[Nobody85]

Спасибо. Теперь мне немного понятнее.