Имеются

и

- произвольные положительные вещественные числа, для которых имеет место неравенство

при любом положительном вещественном

. Как показать, что для рассматриваемых чисел

и

выполняется неравенство
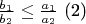
?
Хотел провести доказательство от противного. То есть предположить, что для некоторых

и

выполняется неравенство

и найти

при котором будет нарушаться (1). Но сделать это не смог.
Говоря иначе хотелось бы доказать следующее утверждение:
Пусть

и

- произвольные положительные вещественные числа, для которых имеет место неравенство

при любом положительном вещественном

. Тогда имеет место неравенство
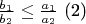
.
Дайте, пожалуйста, подсказку.
Спасибо!