F - артиново коммутативное кольцо с 1
R - артинова слева алгебра над F

Умножение в R' устроено таким образом:
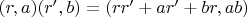
,

,

.
Доказать, что F' - артинова слева алгебра над F.
Т.е., нужно доказать, что идеал F' конечно порожден или доказать, что цепочка идеалов стабилизируется на некотором шаге.
Из этого условия я могу вытащить, что факторы F и R артиновы, множества левых идеалов F и R имеют минимальные элементы.
Но как от этого придти к утверждению?