Уважаемый Someone, хорошо решение уравнения

это

его нужно добавить в ответ если я верно Вас понял, (но в учебнике он не указан).
Обозначим

, получим однопараметрическое семейство решений

. Число

может быть любым. (Кстати, логарифм кодируется как \ln; аналогично \lg, \log, \sin и т.п.)
Случай, если

дает

так?
При

после разделения переменных получаем

, откуда интегрированием получаем

. Выражаем

:

. Из Вашего это получается, если обозначить

.
3. Модуль под знаком логарифма, т.е. вообще говоря это неправильно? Там просто произведение стоит константы

-- нам говорили, что в этом случае мы считаем константу какой угодно и должны навесить внешний модуль (если речь идет об абстрактном примере, не привязанном к физической задаче), или я неправильно это понимаю?
Не надо относиться к этому столь формально. Следует иногда и задумываться. Интегрируя уравнение

получим

(в качестве произвольной постоянной мы можем использовать любое выражение, принимающее все значения, допустимые для решений уравнения). Умножая на

и потенцируя, получим

Снимаем модули; появляющийся при этом знак "

" включаем в определение константы

:

Убрать модуль вокруг

мы не можем, так как это приводит к потере решений в области

.
Далее выражаем

, подставляем

и находим

откуда получаем общее решение

каким образом здесь может появиться модуль вокруг дроби?
4. Если ответ сходится с моим (с учетом опечатки), значит решение верно

Есть ещё один вариант: ответ в задачнике такой же неправильный, как и Ваш. Не думайте, что такой случай является исключительным. Избавиться от всех ошибок и опечаток в столь большой книге практически невозможно.
В данном случае можно заметить, что решения

получаются из общего решения при
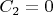
, если обозначить

. Поэтому в ответе мы должны указать

, где

, и

.



