[комбинаторика][ДМ][easy]Правильно ли решил?

[Deffe]

Готовлюсь к экзамену по дискретной математике, прорешиваю задачи, а проверить правильность никак не могу. Буду благодарен, если укажете на ошибки, буду искать ошибки в решении, которое целиком здесь не выкладываю, т.к. много писать.

1. На почте продаются конверты 5 видов и марки 4 видов. Сколько способов покупки 4-х конвертов и 5–ти марок?
   Ответ: $4\cdot5\cdot7\cdot7\cdot8$
   
2. Сколько делителей у числа 8400?
   Ответ: $2\cdot2\cdot3\cdot5$
   
3. В концертной программе шесть номеров: А ,Б, В, Г, Д , Е . Сколько способов составить программу концерта так, чтобы номер Б через один номер после номера А?
   Ответ: $2\cdot3\cdot4\cdot4$
   
4. Чему равна сумма всех пятиразрядных чисел образованных перестановками цифр 1,3,5,7,9?
   Ответ: $5!$
   
5. Сколько способов раскладки 7 различных дискет по трем различным коробкам, в каж-дой из которых имеется по 6 различных отсеков, вмещающих по одной дискете?
   Ответ: $\frac{18!}{9!}$
   
6. Сколько способов выбрать в студенческой группе из 25 человек старосту, профорга и трех членов профбюро?
   Ответ: $\frac{25!}{19!\cdot3!}$
   
7. В магазине продаются 5 видов хлеба и 6 марок минеральной воды. Сколько способов покупки 4-х булок хлеба и 3-х бутылок воды ?
   Ответ: $4\cdot7\cdot7\cdot8$
   
8. Чему равна сумма всех чисел, полученных перестановками цифр числа 1433?
   Ответ: $22$
   
9. Сколько способов раскладки пяти одинаковых монет по трем карманам? В скольких
   случаях хотя бы один карман пуст?
   Ответ: $3^{4}, 2^{5} $
   
10. Сколько способов рассадки 4 пассажиров в купе поезда (по 4 места на двух диванах)
    так, чтобы А сидел по ходу поезда, а пассажиры Б и В рядом?
    Ответ: $36$
    
11. Чему равно $\left | P_{0}(n)\cup P_{1}(n) \right |$?
    $P_{0}(n)$ - множество булевых функций, сохраняющих ноль, $P_{1}(n)$ - сохраняющих еденицу
    Ответ: $3\cdot2^{2^{n}-2}$
    
12. Чему равно $\left | P_{0}(n)\cap P_{1}(n) \right |$?
    Ответ: $2^{2^{n}-2}$

[svv]

У меня получилось:
70 способов купить 4 конверта 5 видов
1111 1112 1113 1114 1115 1122 1123 1124 1125 1133
1134 1135 1144 1145 1155 1222 1223 1224 1225 1233
1234 1235 1244 1245 1255 1333 1334 1335 1344 1345
1355 1444 1445 1455 1555 2222 2223 2224 2225 2233
2234 2235 2244 2245 2255 2333 2334 2335 2344 2345
2355 2444 2445 2455 2555 3333 3334 3335 3344 3345
3355 3444 3445 3455 3555 4444 4445 4455 4555 5555

56 способов купить 5 марок 4 видов
11111 11112 11113 11114 11122 11123 11124 11133
11134 11144 11222 11223 11224 11233 11234 11244
11333 11334 11344 11444 12222 12223 12224 12233
12234 12244 12333 12334 12344 12444 13333 13334
13344 13444 14444 22222 22223 22224 22233 22234
22244 22333 22334 22344 22444 23333 23334 23344
23444 24444 33333 33334 33344 33444 34444 44444

Соответственно, и общее количество не такое, как у Вас.

[Deffe]

svv
И всего, соответственно $70\cdot56=3920$.
У меня почему-то в два раза больше. где-то на двойку не сократил. Пересчитал по формуле $\binom{n-1}{m+n-1}$ сочетания с повторениями еще раз, получилось как у вас.
Спасибо!

[--mS--]

Теперь верно (a), (b), (c), (j). За последние две не знаю, остальные неверно.

-- Вс июн 16, 2013 23:33:06 --

(k) тоже верно.

-- Вс июн 16, 2013 23:33:32 --

Ну и (l) тоже верно.

[Deffe]

--mS--, благодарю!

Перерешал некоторые:
(d) не увидел что "сумма". Oтвет $11111\cdot600$
(e) считал все отсеки различными. Решил, учитывая только то, в какую коробку попала дискета. Oтвет $3^{10}$
(f) $7\cdot11\cdot23\cdot24\cdot25$
(g) решаю по той же формуле, что и (a). Получаю $\binom{3}{8}\cdot\binom{2}{8}$
(h) $1111\cdot48$
(i) $3^5, 2^5$

[--mS--]

Deffe в сообщении #737390 писал(а):

(d) не увидел что "сумма". Oтвет $11111\cdot600$
(h) $1111\cdot48$

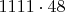
Скорее всего. Тут мне лень считать.

Deffe в сообщении #737390 писал(а):

(e) считал все отсеки различными. Решил, учитывая только то, в какую коробку попала дискета. Oтвет $3^{10}$

В условии различно всё. А этот ответ ни с какой точки зрения не понятен.

Deffe в сообщении #737390 писал(а):

(f) $7\cdot11\cdot23\cdot24\cdot25$
(g) решаю по той же формуле, что и (a). Получаю $\binom{3}{8}\cdot\binom{2}{8}$

(f) верно, а (g) - нет. Вы неправильно применяете формулу.

Deffe в сообщении #737390 писал(а):

(i) $3^5, 2^5$

Монеты одинаковы, а Вы считаете для различных.

[Deffe]

--mS--
Спасибо, теперь все ясно, дальше разберусь.