Итак, вы утверждаете, что..
Итак, я утверждаю, что...
1) в своем решении
espe подменил оператор

(обозначенный у
Widia как

) на оператор

, который ни в коей мере не равен

. В частности,

коммутирует с любой постоянной матрицей, чего не скажешь про

. Да и вообще, пространство функций, на котором действует оператор

, может быть произвольным, например -- скалярные функции. Но даже в теории Дирака операторы

и

не равны друг другу.
2) Нахождение коммутатора сводится к нахождению действия

на функцию координат

. Для этого вспомним определение
Цитата:
Пусть

-- оператор, собственные функции которого

образуют полный набор,

. И пусть

-- некоторая однозначная функция переменной

. Тогда оператором
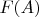
называется такой оператор, для которого

-- полный набор сф с собственными значениями

, т.е.

. При этом, если

-- произвольная функция, то

(1).
Таким образом, чтобы найти действие

на заданную функцию координат нужно разложить эту функцию по собственным векторам оператора

т.е. по плоским волнам и воспользоваться (1). Именно это и было сделанно в моем решении.