Площади тр-ов на графике

[Keter]

Обнаружил одну штуку. Если к $y^2=2px$ провести три касательных в точках $X_1, X_2, X_3,$ то касательные попарно пересекутся в точках $K_1, K_2, K_3.$ Так вот $S_{K_1 K_2 K_3}=\dfrac{1}{2} S_{X_1 X_2 X_3}.$ И так всегда.. Это известный факт? Где можно посмотреть док-во?
Сам доказал через составление уравнений касательных, нахождение координат точек $K_1, K_2, K_3$ и вычисления площадей треугольников через определитель (по трём точкам). Но это слишком долгий путь. Уверен, что где-то это было и должно быть по-легче док-во.

[nnosipov]

Такое ощущение, что это ещё Архимед знал. Можно порыться в какой-нибудь историко-математической литературе, возможно, и сыщется.

[Keter]

nnosipov, рылся, но ничего путного не нашел, кроме площади сегмента...
Хочется увидеть нормальное решение, а то у меня всё как-то тупо в лоб

[Legioner93]

Keter
Ваше соотношение очевидным образом следует из того факта, что площадь сегмента параболы равна удвоенной площади части плоскости, образованной этими касательными и дугой параболы.

Этот известный факт доказал действительно Архимед. Вот геометрическое доказательство (не знаю, такое ли было у Архимеда).

-- Вт июн 11, 2013 18:58:34 --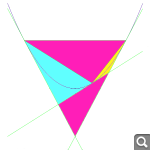


$\frac{S_{\text{верхнего голубого куска}}}{S_{\text{нижнего голубого куска}}}=2$
$\frac{S_{\text{верхнего жёлтого куска}}}{S_{\text{нижнего жёлтого куска}}}=2$
$\frac{S_{\text{верхнего голубого куска}}+S_{\text{верхнего жёлтого куска}}+S_{\text{верхнего фиолетового куска}}}{S_{\text{нижнего голубого куска}}+S_{\text{нижнего жёлтого куска}}+S_{\text{нижнего фиолетового куска}}}=2$
Отсюда и получаем соотношение на площади фиолетовых треугольников $2:1$

(Оффтоп)

Ещё школе обнаружил, что площадь сегмента параболы $y=x^2$ равна $\frac{(x_2 - x_1)^3}{6}$, то есть зависит лишь от расстояния по $x$ между точками. Чему очень удивился

[Keter]

Legioner93, спасибо. Довольно интересно!