Тао о разных математиках.

[пианист]

В блоге Гауэрса, в сообщении о присуждении премии Абеля Делиню развернулась забавная дискуссия.
В числе прочего, Тао там высказал такую мысль:

Цитата:

To summarise: the more algebraic areas of mathematics are generally in the business of establishing ever-stronger lower bounds on the amount of structure present in some mathematical object of interest, whereas the more analytic areas of mathematics are generally in the business of establishing ever-stronger upper bounds on such structure, and nowadays there are now many areas of mathematics in which there is a crucial interplay between the two sides. But it would be a mistake to judge the stature of one of these sides of mathematics through the lens of the other, either by dismissing analysis through its lack of new structures discovered, or dismissing algebra through the lack of new upper bounds discovered.

Т.е.: концептуальные математики пыхтят, отыскивают конструкции, позволяющие компактифицировать длинные и сложные доказательства, делая эти доказательства простыми и очевидными, в то время как не-концептуальные, повелители, так сказать, живого вакуума, которым эти костыли без надобности, напротив, кладут предел усилиям своих коллег.
Интересно, что думают здешние математики по этому поводу?

[Munin]

пианист в сообщении #734594 писал(а):

Т.е.: концептуальные математики пыхтят, отыскивают конструкции, позволяющие компактифицировать длинные и сложные доказательства, делая эти доказательства простыми и очевидными, в то время как не-концептуальные, повелители, так сказать, живого вакуума, которым эти костыли без надобности, напротив, кладут предел усилиям своих коллег.

Кажется, это ваше "т. е." - и есть то самое "judging the stature of one of these sides through the lens of the other", от которого предупреждал Тао.

Кроме того, я не могу с-map-ить вашу формулировку на исходную.

пианист в сообщении #734594 писал(а):

Интересно, что думают здешние математики по этому поводу?

Приношу извинения, что вмешиваюсь.

[longstreet]

Да, ссылки в любом случае не хватало:
http://gowers.wordpress.com/2013/03/20/pierre-deligne-wins-the-2013-abel-prize/

[Munin]

longstreet
Спасибо, очень интересно! (при том, что для меня sowa авторитет)

[longstreet]

(Оффтоп)

Munin в сообщении #734638 писал(а):

для меня sowa авторитет

Единственный на свете? xD Или в паре с Фейнманом?

[Munin]

(Оффтоп)

longstreet в сообщении #734642 писал(а):

Единственный на свете? xD Или в паре с Фейнманом?

В паре, в паре xD На самом деле, просто персонаж, разбирающийся в том, о чём говорит. Поэтому, его высказывания в этом блоге интересны.

[пианист]

Munin
Обсуждение было довольно-таки эмоциональным, и при этом не имело перспектив точного однозначного решения поставленных вопросов. В такой ситуации сложно остаться объективным. Высказал я свое впечатления не только от именно приведенной фразы, но, скорее, от всей дискуссии (спасибо longstreet за ссылку).

(Оффтоп)

Munin в сообщении #734615 писал(а):

Приношу извинения, что вмешиваюсь.

Математики в широком смысле слова :) Ваше мнение мне, безусловно, интересно.

[Munin]

пианист
Приношу извинения за поспешное мнение. По ссылке
http://owl-sowa.blogspot.ru/2012/05/my- ... owers.html
даны пояснения, кто такие "концептуальные математики", и мне надо это осмыслить. Пока не высказываюсь.

-- 09.06.2013 19:38:04 --

Если мне позволено будет высказать свою формулировку, то мне кажется, что sowa ясно противопоставляет несколько иные вещи: содержательные результаты, с одной стороны, и "методы грубой силы", с другой. Это не "алгебраисты и аналитики", а разные виды вкладов в математическое знание. Содержательные результаты связывают одни области математики с другими, строят новые понятийные системы, и тем самым бросают новый свет на проблемы, с которыми имеют дело. А "методы грубой силы" разбираются с проблемами скучно и неэффективно. Они могут доказывать факт, который будет широко использоваться, но не поведут никуда вперёд тех, кто использует этот факт, и по сути, ничего не говорят нового об этом факте, кроме того, что он верен или неверен.

[Munin]

Мне показалось, что предыдущий текст Tao ценен, по крайней мере, тем, что помогает понять, о чём его вывод, и вводит те понятия, которые в выводе используются. Извините за большую цитату:

Цитата:

The example of elliptic integrals and elliptic curves, to me, is actually quite a good example of what structured mathematics is, and what its boundaries are. We have many examples of the beautiful crystalline structure of the mathematics surrounding elliptic curves being replaced by the quite different (but to my mind, still very beautiful) disorder and anti-structure when one tries to move to more general mathematical settings. For instance, when solving completely integrable equations such as the periodic Korteweg-de Vries equation, there are a beautiful set of special solutions (coming from finite gap potentials) in which the equation can be solved exactly using elliptic integrals (or more precisely, Abelian integrals which are a hyperelliptic variant), giving quasiperiodic solutions. However, when one moves to arbitrary data (with infinitely many gaps in the spectrum of the associated Lax operator), then the situation is now a nonlinear version of a Fourier series with arbitrary coefficients, and is as chaotic and disordered as one would expect from Fourier analysis. Nevertheless, we can still extract finite gap approximants to such infinite gap solutions, thus seeing the core structured behavior amidst the general chaos. In nonperiodic settings the analogue would be what is (conjecturally, at least) a “resolution of solitons” phenomenon in which the structured component and the radiative component of the solutions can be separated asymptotically in the limit, which is a sort of nonlinear version of the way that the spectral theorem can distinguish discrete spectrum from continuous spectrum. Again, the radiative component is not structured at all, being again like an arbitrary Fourier integral, and it complements the structure of the soliton component rather than being somehow “inferior” or “softer” than it. The interplay between structured components of a PDE (e.g. ground state solitons) and radiative or perturbative components is an incredibly rich subject, requiring a combination of both structured mathematics and unstructured analysis; to loosely quote Tolstoy, “true life is lived when tiny changes occur”.

Or: the rational points on an elliptic curve have an enormous amount of deep structure, of course, starting with the basic fact that they form a finite rank abelian group. But when one moves to higher genus what one sees instead is antistructure: the structure of an integer point in a higher genus curve has the tendency to destroy or repel most other possible integer points, which is what ultimately leads to results such as Faltings’ theorem (Mordell conjecture) on such curves. This type of result is much closer in spirit to what comes out of what Grothendieck called the “arid steppes” of analysis (such as Fourier analysis): analysis tells us that when analysing the Fourier coefficients of an arbitrary function, then it is occasionally possible to have a single large Fourier coefficient (which, in this context, is the structure playing the role of an integer point on a high genus curve), but this type of structure tends to repel other such structures, so that a given function cannot have too many large Fourier coefficients at once. To encapsulate this fundamental antistructure phenomenon one needs tools from analysis (in this case, things like the Plancherel identity or Bessel’s inequality) than from the structured side of mathematics. And we know from various “no go” theorems (e.g. Matiyasevich’s theorem, unsolvability of the quintic by radicals, etc.) that once one’s varieties reach a certain level of complexity, it is no longer reasonable to expect the same paradise of structure that elliptic curves enjoy in abundance. This is not just a reflection of the relative state of development of the genus one and higher genus theory, or of the relative “depth” or “importance” of each one; it is a fundamental distinction arising from the nature of mathematics itself.

The story of Szemeredi’s theorem and its variants can be viewed as a struggle to usefully separate out the structured and unstructured components of a mathematical object, in this case a set of integers and the additive patterns it contains. The way my first result with Ben worked, we were able to use tools from combinatorics and analysis to show that the primes could essentially have only a bounded number of structures in them that could influence the number of arithmetic progressions it contained, because each such structure tended to repel all the others. And then we used Szemeredi’s theorem to conclude that no matter where these bounded number of structures were distributed, arithmetic progressions would necessarily be generated. As correctly noted above, this is a result more about progressions than about primes (my coauthor, Ben Green, tends to stress this point in his own expositions, e.g. in Section 2 of http://arxiv.org/pdf/math/0508063v1.pdf ).

In my later work with Ben (and also Tamar Ziegler) on generalising this result to further additive patterns and to obtain precise asymptotics on the counts for these patterns, the primes play a more essential role. Firstly, one has to use deeper tools from analysis (in this case, the inverse conjectures for the Gowers norms) to make the “bounded number of structures” mentioned earlier far more algebraic, and in particular to give them the structure of a nilsystem. Then, in order to keep the primes additively disjoint from such nilsystems, one now has to exploit the antistructure effect encoded by the multiplicative structure of the primes, which tends to repel additive structure (this is yet another variant of the sum-product phenomenon mentioned in previous comments). Roughly speaking, when the nilsystem is coming from an “irrational” shift, then one can use the Vinogradov-Vaughan method of bilinear sums to formalise this repulsion between multiplicative and additive structure. In the case of rational shifts, one instead has to use the classical device of L-functions, and ultimately turn to Siegel’s theorem on the zeroes of such L-functions, which again ultimately boils down to an antistructure phenomenon in which one L-function zero close to 1 tends to repel all other such zeroes. At the end of the day, it is true that our arguments do not discover any new structure on the primes beyond the multiplicative structure that was already known to be present – but then again, all our conjectures about the primes (e.g. the Mobius randomness conjecture) point to the fact that no further such structure should be expected (at least within the additive framework considered here), and instead it is the antistructure of the primes which we have been able to shed some new light on rather than the structure of the primes. Again, this antistructure is an actual feature of the primes (particularly when they are viewed additively) and is not likely to be supplanted by a structured viewpoint in any time in the near future. (Even in the function field setting, for instance, where there is substantially more structure as evidenced for instance by the Weil conjectures, the primes (i.e. irreducible polynomials) are still extremely anti-structured, with only a very small minority of primes in this case being able to be manipulated explicitly (though this situation is much better than in the rational case in which we cannot really get our hands on a single large prime at all). This small set of structured primes in the function field world is enough to solve some qualitative problems that the rational case cannot (e.g. the twin prime conjecture is known in function fields), but for quantitative conjectures such as the asymptotics for twin primes, the situation is essentially just as difficult as in the rational case.)

-- 11.06.2013 04:37:06 --

В частности, первый пример (с уравнением КдФ) мне показался смутно понятным, и если бы кто-нибудь взялся объяснить его ещё более простым языком, я был бы признателен.

[Munin]

Мне понравилось вот это пояснение sowa http://owl-sowa.blogspot.ru/2013/03/rep ... owers.html

Цитата:

Let me clarify how I understand the term “conceptual”. A theory is conceptual if most of the difficulties were moved from proofs to definitions (i.e. to concepts), or they are there from the very beginning (which may happen only inside of an already conceptual theory). The definitions may be difficult to digest at the first encounter, but the proofs are straightforward. A very good and elementary example is provided by the modern form of the Stokes theorem. In 19th century we had the fundamental theorem of calculus and 3 theorems, respectively due to Gauss-Ostrogradsky, Green, and Stokes, dealing with more complicated integrals. Now we have only one theorem, usually called Stokes theorem, valid for all dimensions. After all definitions are put in place, its proof is trivial. M. Spivak nicely explains this in the preface to his classics, “Calculus on manifolds”. (I would like to note in parentheses that if the algebraic concepts are chosen more carefully than in his book, then the whole theory would be noticeably simpler and the definitions would be easier to digest. Unfortunately, such approaches did not found their way into the textbooks yet.) So, in this case the conceptualization leads to trivial proofs and much more general results. Moreover, its opens the way to further developments: the de Rham cohomology turns into the most natural next thing to study.

I think that for every branch of mathematics and every theory such a conceptualization eventually turns into a necessity: without it the subject grows into a huge body of interrelated and cross-referenced results and eventually falls apart into many to a big extent isolated problems.

[Vince Diesel]

пианист в сообщении #734594 писал(а):

В блоге Гауэрса, в сообщении о присуждении премии Абеля Делиню развернулась забавная дискуссия.
В числе прочего, Тао там высказал такую мысль:

Цитата:

To summarise: the more algebraic areas of mathematics are generally in the business of establishing ever-stronger lower bounds on the amount of structure present in some mathematical object of interest, whereas the more analytic areas of mathematics are generally in the business of establishing ever-stronger upper bounds on such structure, and nowadays there are now many areas of mathematics in which there is a crucial interplay between the two sides. But it would be a mistake to judge the stature of one of these sides of mathematics through the lens of the other, either by dismissing analysis through its lack of new structures discovered, or dismissing algebra through the lack of new upper bounds discovered.

Т.е.: концептуальные математики пыхтят, отыскивают конструкции, позволяющие компактифицировать длинные и сложные доказательства, делая эти доказательства простыми и очевидными, в то время как не-концептуальные, повелители, так сказать, живого вакуума, которым эти костыли без надобности, напротив, кладут предел усилиям своих коллег.
Интересно, что думают здешние математики по этому поводу?

Я понял этот текст (и предыдущие примеры) по-другому. Одни математики (алгебраисты) отыскивают (алгебраические) структуры у любого изучаемого объекта. И, таким образом, находят "оценки снизу" на структурированность объекта. Аналитики же рассматривают объекты, сложно поддающиеся структуризации и устанавливают всякие результаты, говорящие, в частности, что такой-то объект сложен, простой алгебраической структурой не описывается. Скажем, хаотическое поведение решений некоторых систем уравнений. Тао называет это "оценки сверху на структурированность". В качестве примера он приводит уравнение Кортевега-де Фриза. В некоторых простых случаях, несмотря на нелинейность уравнения, можно выписать решение явно. При этом используются скрытые симметрии уравнения КдФ (как указывается, оно является вполне интегрируемым). В общем же случае такого алгебраического описания решений получить не удается и вряд ли стоит на это надеяться. Тем не менее можно получать приближения решения общего вида хорошими. Так я понимаю эти слова об "interplay between the two sides" - о взаимодействии в одном объекте того, что можно структурировать и тем, что простой структуризации не поддается.

[Munin]

Теперь мне ясно, что значит "концептуальные математики", но недостаточно ясно, что подразумевал Tao в своём выводе о "the more algebraic areas / the more analytic areas of mathematics". Кроме того, я явно упускаю, что кроется за словами "the crystalline structure", "crystal" - похоже, это какой-то термин. Any help will be appreciated.

-- 11.06.2013 13:45:42 --

Вот пояснение sowa, которое я нашёл:

Цитата:

When you move from SL(n) for n>2 to SL(2), you are usually change the branches of mathematics. I do not think that a theorem not dealing with the SL(2) case is in any sense incomplete. There is similarly sounding problem in another branch of mathematics, but this does not diminishes the significance of your result. SL(2,Z) is essentially free group, and, as somebody said, a free group is not a group, but just a collection of words (there is a reference for this maxim, but it is attributed there to “somebody”). Of course, by moving to SL(2,Z) you are leaving the realm of crystal-like groups and enter an amorphous area where methods of combinatorics appear to be more suitable.

Это какое-то явное указание на термин.

-- 11.06.2013 13:47:38 --

Очень жаль, что, похоже, обсуждаемые пассажи Tao остались без комментариев sowa, это было бы интересно.

(Оффтоп)

Попросить его, что ли, прокомментировать...

[Vince Diesel]

Munin в сообщении #735347 писал(а):

Теперь мне ясно, что значит "концептуальные математики", но недостаточно ясно, что подразумевал Tao в своём выводе о "the more algebraic areas / the more analytic areas of mathematics". Кроме того, я явно упускаю, что кроется за словами "the crystalline structure", "crystal" - похоже, это какой-то термин

По поводу алгебраических/аналитических областей, как я понял это, написал выше. А кристаллическая решетка здесь, имхо, просто метафора. С ней сравниваются алгебраические структуры, как нечто наиболее упорядоченное. И противопоставляется беспорядок и хаос других математических объектов.

Munin в сообщении #735344 писал(а):

Мне понравилось вот это пояснение sowa http://owl-sowa.blogspot.ru/2013/03/rep ... owers.html

Цитата:

Let me clarify how I understand the term “conceptual”. A theory is conceptual if most of the difficulties were moved from proofs to definitions (i.e. to concepts), or they are there from the very beginning (which may happen only inside of an already conceptual theory).

В той же дискуссии у Гауэрса упоминается изречение, приписываемое Манину: "доказательства важнее теорем, определения важнее доказательств". Также я встречал еще одно высказывание Манина: "за каждым определением стоит работа поколений математиков". Как-то так, не ручаюсь за дословность.

[Munin]

Хотя это и совсем в стороне от обсуждаемой темы, но интересное мнение sowa, которое обратило на себя моё внимание, и которое я хочу процитировать:
What is mathematics?

Цитата:

Let me say only point out that mathematics has any value only as human activity. It is partially a science, but to a big extent it is an art. All proofs belong to the art part. They are not needed at all for applications of mathematics. If a proof cannot be understood by humans,... they have no value. Or, rather, their value is negative: a lot of human time and computer resources were wasted.

(Остальная часть поста - развёрнутые пояснения и комментарии к этому тезису, тоже интересные и крайне наглядные, но я не хочу перегружать данную тему цитированием офтопика.)

(Оффтоп)

Лично мой комментарий: в таком смысле, в любой science есть составляющая art: это та часть science, которая составляет идеи, и движет scientists к новым достижениям. Это необыкновенно важная часть science, но лично я не склонен отделять её от science вообще: без неё science мертва, и просто вырождается в collection of known facts. 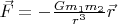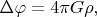Например, две формулировки теории тяготения Ньютона, $\vec{F}=-\tfrac{Gm_1m_2}{r^3}\vec{r}$ и $\Delta\varphi=4\pi G\rho,$ эквивалентны для вычислений, но совершенно не равнозначны для науки: они ведут к разным теоретическим модификациям и обобщениям. Они отличаются тем, что в вышеупомянутом обсуждении называлось conceptual framework и conceptual context.

-- 11.06.2013 14:38:27 --

Vince Diesel в сообщении #735363 писал(а):

По поводу алгебраических/аналитических областей, как я понял это, написал выше.

Да, спасибо, ваши пояснения почти проясняют пассаж Тао о КдФ для меня целиком. Видимо, неясными остаются только незначительные моменты. Я ещё перечитаю.

Vince Diesel в сообщении #735363 писал(а):

В той же дискуссии у Гауэрса упоминается изречение, приписываемое Манину: "доказательства важнее теорем, определения важнее доказательств".

Да, и неоднократно (и приводит его, в основном, тоже sowa, так что в отрывке о слове “conceptual” к этому изречению идёт явная отсылка. Я хотел процитировать, но не дошли руки. Спасибо!

Vince Diesel в сообщении #735363 писал(а):

Также я встречал еще одно высказывание Манина: "за каждым определением стоит работа поколений математиков". Как-то так, не ручаюсь за дословность.

Ценно, хотя вариация того же самого.

Vince Diesel в сообщении #735363 писал(а):

А кристаллическая решетка здесь, имхо, просто метафора. С ней сравниваются алгебраические структуры, как нечто наиболее упорядоченное. И противопоставляется беспорядок и хаос других математических объектов.

Кажется, я понял, в чём дело. Я думал про "кристалл" с точки зрения его внешней формы - красивого многогранника - а вовсе не с точки зрения кристаллической решётки :-) В этом смысле, как эпитет this makes much more sense. Спасибо!

-- 11.06.2013 15:08:09 --

Продолжение на ту же тему (похоже, Vince Diesel заинтересовался) в посте sowa
The conceptual mathematics vs. the classical (combinatorial) one.
Опять, в качестве аннотации приведу только небольшую цитату:

Цитата:

It is not easy to explain how conceptual theorems and proofs, especially the ones of the level close to the one of Grothendieck work, could be at the same time more easy and more difficult at the same time. In fact, they are easy in one sense and difficult in another. The conceptual mathematics depends on – what one expect here? – on new concepts, or, what is the same, on the new definitions in order to solve new problems. The hard part is to discover appropriate definitions. After this proofs are very natural and straightforward up to being completely trivial in many situations. They are easy. Classically, the convoluted proofs with artificial tricks were valued most of all. Classically, it is desirable to have a most elementary proof possible, no matter how complicated it is.

A lot of efforts were devoted to attempts to prove the theorem about the distribution of primes elementary. In this case the requirement was not to use the theory of complex functions. Finally, such proof was found, and it turned out to be useless. Neither the first elementary proof, nor subsequent ones had clarified anything, and none helped to prove a much more precise form of this theorem, known as Riemann hypothesis (this is still an open problem which many consider as the most important problem in mathematics).

Остальная часть поста демонстрирует те же идеи на примере теоремы Стокса, и завершается ещё несколькими обобщающими словами.

[пианист]

Munin
Тао имеет в виду задачу с периодическими краевыми условиями (конечнозонные решения). Там фишка такая: расставляем точки спектра оператора Лакса уравнения по комплексной плоскости - это д.б. точки ветвления, проводим, соот-но, разрезы, склеиваем риманову поверхность; так вот, из соответствующих такой римановой поверхности тэта-функций и получается решение, и вот это-то (что тэта-функции) и есть Красота и Гармония :)
Но это все, когда точек спектра конечно, т.е. вырожденный случай, в общем же (общем по начальным условиям) их бесконечно; проинтегрировать все равно можно, видимо, там получается что-то аналогичное интегралу Гельфанда-Левитана для быстроубывающего случая
(поправьте, кто в теме), но вот Красоту уже не получим :)
И еще нюанс: в быстроубывающем случае произвольное решение через какое-то время разваливается на солитоны; видимо, в периодическом случае есть что-то аналогичное.